A Casinha da Matemática Blog
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 11 Ex. 4
Enunciado
Um triângulo retângulo [ABC], em que o cateto [AB] está contido no plano \(\beta \), rodou em torno do outro cateto gerando um cone, como se mostra na figura.
Sabendo que \(\overline {AC} = 4\) cm e que \(\overline {AB} = 3\) cm, determine a distância do ponto C ao plano \(\beta \).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 11 Ex. 3
Enunciado
Considera a seguinte pirâmide quadrangular regular [ABCDV].
Sabemos que:
- a área de cada face lateral é 60 cm2;
- o comprimento da altura de cada face lateral é 10 cm;
- V’ é a projeção ortogonal de V (vértice da pirâmide) no plano ABC.
Calcula a distância de V a V’.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Distâncias, áreas e volumes de sólidos: Matematicamente Falando 9 - Parte 2 Pág. 11 Ex. 2
Enunciado
O ponto P’ é a projeção ortogonal do ponto P no plano \(\alpha \).
A é um ponto do plano \(\alpha \), distinto de P’.
A distância do ponto P ao ponto A é 50 cm e a distância do ponto P’ ao ponto A é 14 cm.
Qual é a distância do ponto P ao plano \(\alpha \)?
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 152 Ex. 3
Enunciado
Na figura está representada uma circunferência de centro no ponto O.
Sabe-se que:
- Os pontos A, B, C, D e E pertencem à circunferência;
- [AD] é um diâmetro da circunferência;
- O ponto P é o ponto de interseção dos segmentos de reta [AC] e [BD];
- \(C\widehat AD = 40^\circ \).
- Qual das afirmações seguintes é verdadeira?
[A] O ponto O pertence à mediatriz do segmento de reta [AP].
[B] O ponto O pertence à mediatriz do segmento
…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 151 Ex. 7
Enunciado
Na figura, está representada uma circunferência de centro no ponto O. Estão também representados o triângulo [AEF] e o quadrado [ABCD], cujos vértices pertencem à circunferência.
- Identifica, usando as letras da figura, dois pontos pertencentes à mediatriz do segmento de reta [BD].
- Sabe-se que a amplitude do ângulo EAF é 60 graus e a amplitude do arco FD é 20 graus.
Determina a amplitude, em graus, do arco BE.
Mostra como chegaste à tua resposta.
Resolução >>… Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 149 Ex. 4
Enunciado
Na figura, estão representados uma circunferência de centro no ponto O e os triângulos [ABC] e [CDE].
Sabe-se que:
- os pontos A, B e C pertencem à circunferência;
- [BC] é um diâmetro da circunferência;
- o triângulo [CDE] é retângulo em E;
- os triângulos [ABC] e [CDE] são semelhantes.
A figura não está desenhada à escala.
- Admite que a amplitude do ângulo ACB é igual a 36 graus.
Qual é a amplitude do arco AB?
- Admite que \(\frac{{\overline
…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 149 Ex. 3
Enunciado
Na figura está representada uma circunferência.
Sabe-se que:
- [AC] é um diâmetro de comprimento 15;
- B é um ponto da circunferência.
- \(\overline {AB} = 12\)
- Justifica que o triângulo [ABC] é retângulo em B.
- Calcula a área da região sombreada a laranja na figura.
Apresenta os cálculos que efetuares e, na tua resposta, escreve o resultado arredondado às unidades.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 145 Ex. 18
Enunciado
Um quadrilátero [ABCD] está inscrito numa circunferência.
Dois dos seus ângulos internos consecutivos têm, respetivamente, 56 e 112 graus de amplitude.
Quais são as medidas das amplitudes dos outros dois ângulos internos do quadrilátero?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 145 Ex. 16
Enunciado
Desenha um hexágono regular inscrito numa circunferência e os raios correspondentes aos extremos de cada um dos lados do hexágono.
- Classifica cada um dos triângulos obtidos.
- Que relação existe entre o comprimento do lado do hexágono e o comprimento do raio da circunferência circunscrita ao hexágono?
- Se a circunferência tiver 5 cm de raio, qual é a área do hexágono nela inscrito?
Apresenta todos os cálculos que efetuares e o valor arredondado às unidades.
Resolução >>
Resolução… Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 145 Ex. 12
Enunciado
Um polígono regular tem 25 lados.
- Qual é a soma das amplitudes dos seus ângulos internos?
- Qual é a amplitude de cada ângulo interno do polígono?
- Qual é a soma das amplitudes dos seus ângulos externos?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 145 Ex. 11
Enunciado
Numa circunferência com 12 cm de raio está inscrito um quadrado.
Determina:
- o perímetro do círculo;
- a área do círculo;
- a área do quadrado;
- a área do setor circular cujo ângulo ao centro tem 90 graus de amplitude.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 145 Ex. 10
Enunciado
Na figura, \(\overparen{AD} + \overparen{BC} = 260^\circ \).
Determina a amplitude do ângulo AVB.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 144 Ex. 9
Enunciado
Sabendo que \(\overparen{AB} = 30^\circ \) e \(\overparen{CD} = 90^\circ \), determina a amplitude do ângulo CPD.
Resolução >>
Resolução
<< Enunciado…
Ler mais
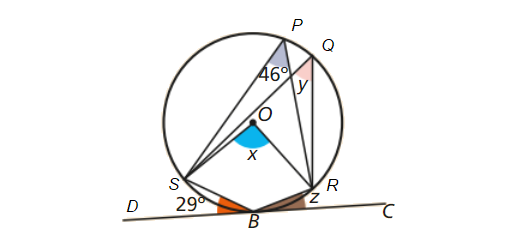
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 144 Ex. 8
Enunciado
A reta BC é tangente à circunferência de centro O.
Quais são os valores das medidas de amplitude x, y e z, dos ângulos assinalados?
Resolução >>
Resolução
<< Enunciado…
Ler mais