A Casinha da Matemática Blog
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 18
Enunciado
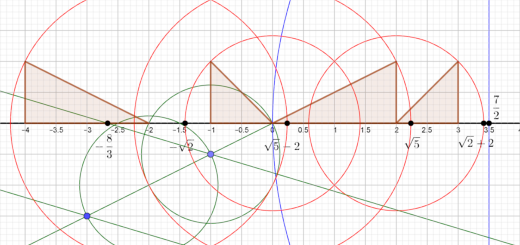
Considera os seguintes números reais:
| \(A \to \frac{7}{2}\) |
\(B \to – \frac{8}{3}\) |
\(C \to \sqrt 5 \) |
| \(D \to – \sqrt 2 \) |
\(E \to \sqrt 2 + 2\) |
\(F \to \sqrt 5 – 2\) |
- Representa os números reais dados numa reta numérica.
- Escreve os números dados por ordem crescente.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 16
Enunciado
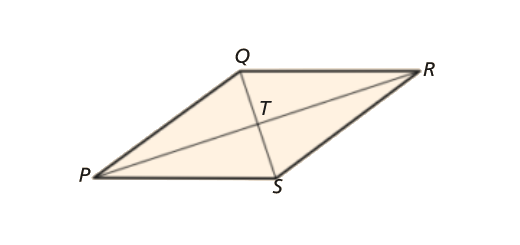
Considera um losango [PQRS], de perímetro 1 m, cujas diagonais se intersetam no ponto T.
Sabendo que [PT] tem 24 cm de comprimento, determina a área do losango.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 67 Ex. 15
Enunciado
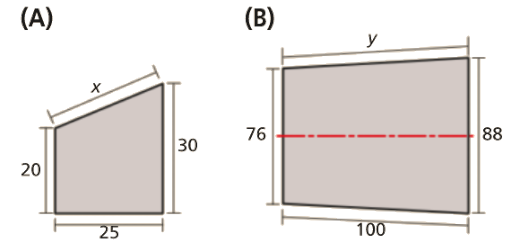
Observa as medidas, em milímetros, das bases de duas peças metálicas com a forma de trapézio.
O segmento de reta a vermelho é eixo de simetria de reflexão da figura (B).
- Determina x e y.
- Calcula o perímetro de cada uma das bases.
- Pretendendo forrar a papel as duas bases, quantos cm2 de papel se vão gastar em cada uma delas?
Apresenta o resultado arredondado às centésimas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 14
Enunciado
Quem chega a Lisboa, entrando pelo Tejo, encontra uma torre “torta”, mas elegante, que alberga o Centro de Coordenação e Controlo de Tráfego Marítimo.
A torre tem a forma de um prisma quadrangular oblíquo. A sua altura é de 36 m, e a torre está inclinada a sul, segundo um ângulo de cerca de 75°. Se o sol incidisse a pique sobre a torre, esta projetaria uma sombra retangular, em que um dos lados mediria, aproximadamente, … Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 13
Enunciado
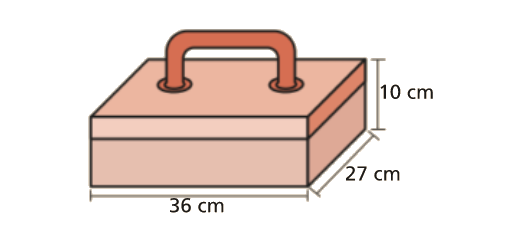
É possível colocar numa caixa de ferramentas, com 36 cm de comprimento, 27 cm de largura e 10 cm de altura, um pedaço de cano metálico de 42 cm de comprimento?
Explica a tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 12
Enunciado
A figura representa a vista lateral de uma rampa.
- Qual é a área da parte lateral da rampa?
- Calcula o comprimento da parte inclinada da rampa.
Resolução >>
Resolução
<< Enunciado…
Ler mais
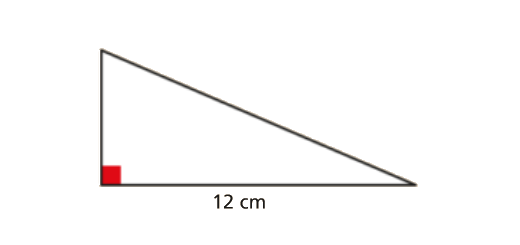
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 11
Enunciado
Considera o seguinte triângulo retângulo.
A área do triângulo é 54 cm2.
Determina o valor exato do seu perímetro.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 66 Ex. 10
Enunciado
Observa o papagaio de papel [ABCD].
\(\overline {AB} = 5,4\) cm; \(\overline {BC} = 8,5\) cm e \(\overline {BD} = 7,6\).
- Calcula o perímetro do papagaio.
- Qual é a área de papel gasto no papagaio?
(Sempre que necessário, usa valores aproximados às décimas.)
Resolução >>
Resolução
<< Enunciado…
Ler mais
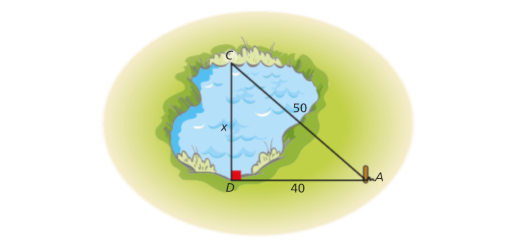
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 9
Enunciado
Fixando uma estaca no ponto A e marcando os pontos C e D nas margens do lago, de modo que o ângulo ADC seja reto, a Catarina verificou que \(\overline {DA} = 40\) m e que \(\overline {AC} = 50\).
Qual é a distância entre os pontos C e D das margens do lago?
Resolução >>
Resolução
<< Enunciado…
Ler mais
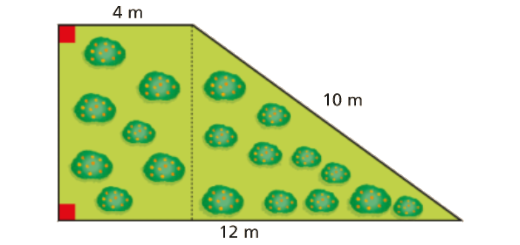
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 8
Enunciado
A D.ª Rosalina possui o pomar representado na figura seguinte.
Determina a área do pomar da D.ª Rosalina.
Resolução >>
Resolução
<< Enunciado…
Ler mais
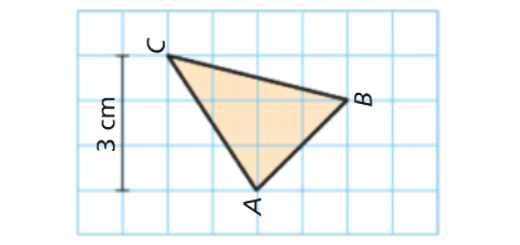
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 7
Enunciado
Determina o perímetro, arredondado às décimas, do triângulo [ABC].
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 6
Enunciado
Um balão publicitário encontra-se preso ao solo por uma corda.
Num dia sem vento, estava suspenso na vertical, a 15 metros de altura. No entanto, no dia anterior esteve muito vento e o balão afastou-se 12 m do local onde se encontrava preso.
A que altura se encontrava?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 5
Enunciado
Qual é a altura de um triângulo equilátero com 18 cm de perímetro?
Resolução >>
Resolução
<< Enunciado…
Ler mais
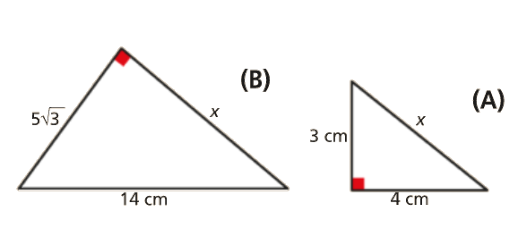
Teorema de Pitágoras: Matematicamente Falando 8 - Pág. 65 Ex. 4
Enunciado
Aplicando o Teorema de Pitágoras, calcula o valor de x em cada caso.
Resolução >>
Resolução
<< Enunciado…
Ler mais