A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Category: Aplicando

0

Aplicando / 10.º Ano / Módulo inicial

Duas esferas e um cilindro

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 37 Ex. 19

Enunciado

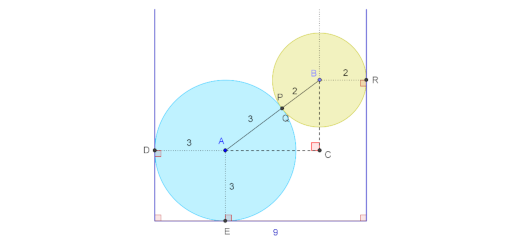
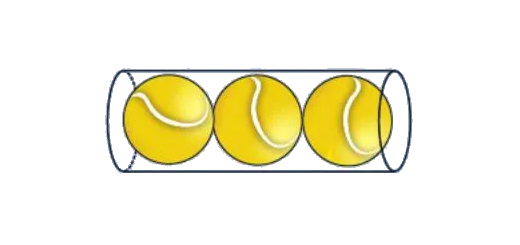
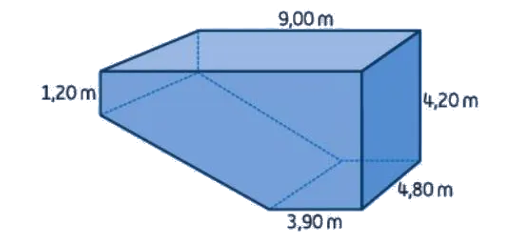
Duas esferas, de raios $2$ e $3$, estão encaixadas num recipiente cilíndrico de diâmetro $9$ (unidades em centímetro).

  1. Faça um desenho e explique a sua construção.  
  2. Qual é o volume de líquido necessário para cobrir totalmente as duas esferas.  
  3. Se o líquido cobrir exatamente a esfera maior, que se encontra no fundo, que parte da esfera menor fica fora?

Resolução >> Resolução

<< Enunciado… Ler mais
0

10.º Ano / Módulo inicial / Aplicando

O caracol e a alface

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 36 Ex. 16

Enunciado

Um caracol colocado em $C$ quer atingir uma alface em $A$.

Para isso, tem de escalar uma placa de vidro [de espessura desprezável], com $0,75$ m de altura.

A distância do caracol à placa é $1,5$ m e da placa à alface é de $1$ m.

Na figura está representado, a vermelho, um exemplo de trajeto que o caracol pode seguir.

Se a sua velocidade é de $5$ km/h, quanto tempo, no mínimo, terá de esperar até … Ler mais

0

Aplicando / 10.º Ano / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 4

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 14

Enunciado

Desenhe um quadrilátero qualquer e o paralelogramo que se obtém unindo consecutivamente os pontos médios dos lados desse quadrilátero.

  1. Suponha que as diagonais do quadrilátero dado medem $10$ cm e $6$ cm.
    Quanto medem os lados do novo quadrilátero?
  2. Confirme que o perímetro do paralelogramo é igual à soma das diagonais do quadrilátero original.
  3. Investigue qual é a relação entre as áreas do quadrilátero dado e a do paralelogramo.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 10.º Ano / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 3

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 13

Enunciado

Unindo os pontos médios dos lados consecutivos de um quadrilátero, podemos obter um trapézio não paralelogramo? E um losango? Em que condições?

Resolução >> Resolução

<< Enunciado… Ler mais
1

Aplicando / 10.º Ano / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 2

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 12

Enunciado

A que condição deve obedecer um quadrilátero convexo para que, unindo os pontos médios dos lados consecutivos, se obtenha:

  1. um retângulo;
  2. um quadrado.

Resolução >> Resolução

<< Enunciado… Ler mais
3

Aplicando / 10.º Ano / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 1

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 24 TAREFA

Enunciado

Determine três, ou mais, quadriláteros como os que se seguem.

  1. Determine os pontos médios dos lados dos quadriláteros e, em cada um deles, construa os segmentos de reta definidos por pontos médios de lados consecutivos.
  2. Investigue que tipo de quadriláteros obteve. Registe as suas conjeturas e tente justificá-las.
  3. Recorrendo a propriedades estudadas, prove, por exemplo, que o polígono que se obtém unindo os pontos médios dos lados consecutivos do quadrilátero [ABCD] é um paralelogramo.

R1 … Ler mais

0

Módulo inicial / Aplicando / 10.º Ano

Caixa de forma cilíndrica com bolas de ténis

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 33 Ex. 11

Enunciado

Uma caixa de forma cilíndrica com bolas de ténis tem $7$ cm de diâmetro e uma altura de $20$ cm.

Se o diâmetro de cada bola de ténis for $6$ cm, qual a percentagem do volume ocupado pelas $3$ bolas?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 10.º Ano / Módulo inicial

A altura do cone

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 33 Ex. 9

Enunciado

O setor circular $ARC$ tem raio $9$ cm e o ângulo mede $80^\circ $.

Quando se corta o setor circular e se junta, com fita adesiva, os segmentos $AR$ e $RC$ forma-se o cone, sem base, representado na figura.

Determine a altura do cone.

Resolução >> Resolução

<< Enunciado… Ler mais
0

10.º Ano / Módulo inicial / Aplicando

Um copo cilíndrico e uma esfera metálica

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 33 Ex. 7

Enunciado

Um copo cilíndrico com $10$ cm de altura e $8$ cm de diâmetro está cheio, com água, até $1$ cm do topo.

Se uma bola metálica com $4$ cm de diâmetro for introduzida no copo, a água será vertida?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 10.º Ano / Módulo inicial

Lúnulas de Hipócrates

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 33 Ex. 6

Enunciado

No século V a.C., viveu, na ilha de Chios, o matemático Hipócrates, que mostrou, pela primeira vez, que uma certa figura limitada por arcos de circunferência tinha uma área igual à de determinado triângulo.

Observe, na figura, o triângulo [ABC], retângulo em A.

Mostre que a área colorida (lúnulas) é igual à área do triângulo.

Pode, então, concluir que nem sempre aparece o número $\pi $, para calcular áreas de figuras em que intervêm círculos.

Resolução … Ler mais