A turma da Maria José
Estatística e probabilidades: Matematicamente Falando 9 - Parte 1 Pág. 23 Ex. 18
Enunciado
Foi feito um inquérito aos 28 alunos da turma da Maria José sobre os desportos que praticavam.
Concluiu-se que 15 praticavam futebol e 16 basquetebol. (Qualquer aluno da turma pratica pelo menos uma dessas modalidades.)
Qual é a probabilidade de, escolhido um aluno da turma ao acaso, ele praticar:
- futebol e basquetebol?
- futebol mas não basquetebol?
- basquetebol mas não futebol?
Resolução
Sejam T, F e B, respetivamente, o conjunto dos alunos da turna, o conjunto dos alunos que praticam futebol e o conjunto dos alunos que praticam basquetebol.
Ora, sabe-se que:
- A turma tem 28 alunos, logo $\#T=28$;
- 15 alunos praticam futebol, logo $\#F=15$;
- 16 alunos praticam basquetebol, logo $\#B=16$.
Como qualquer aluno da turma pratica pelo menos uma dessas modalidades e $\#F+\#B+0=15+16=31$, conclui-se que 3 alunos praticam as duas modalidades, isto é, $\#(F\cap B)=3$.
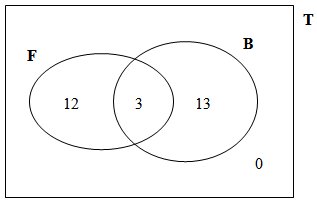
Esta conclusão conjuntamente com os dados do problema permitem elaborar o diagrama apresentado ao lado.
- Logo, $P(\text{”praticar futebol e basquetebol”})=\frac{3}{28}$.
- Logo, $P(\text{”praticar futebol mas n }\!\!\tilde{\mathrm{a}}\!\!\text{ o basquetebol”})=\frac{12}{28}=\frac{3}{7}$.
- Logo, $P(\text{”praticar basquetebol mas n }\!\!\tilde{\mathrm{a}}\!\!\text{ o futebol”})=\frac{13}{28}$.
