A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Tagged: 11.º Ano

0

Aplicando / 11.º Ano / Operações com funções

Três funções: $f$, $g$ e $\frac{f}{g}$

Mais funções: Aleph 11 - Volume 2 Pág. 125 Ex. 10

Enunciado
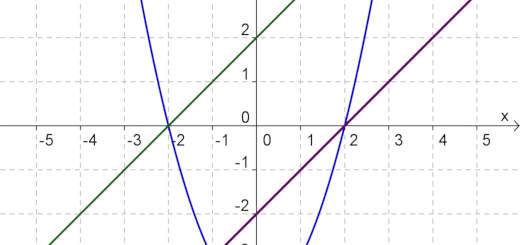
Sejam $f$ e $g$ duas funções definidas por: \[\begin{array}{*{20}{c}}
{f\left( x \right) = {x^2} – 4}&{\text{e}}&{g\left( x \right) = x + 2}
\end{array}\]

Caracterize a função $\frac{f}{g}$ e estude o seu sinal, relacionando-o com o sinal quer da função $f$ quer da função $g$.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Operações com funções

Duas funções, $s$ e $t$

Mais funções: Aleph 11 - Volume 2 Pág. 122 Ex. 9

Enunciado

Na figura estão representadas graficamente as funções $s$ e $t$.

Determine:

  1. $s\left( 0 \right)$
  2. $t\left( 5 \right)$
  3. $\left( {s + t} \right)\left( 3 \right)$
  4. $\left( {s – t} \right)\left( 3 \right)$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Operações com funções

Verifique se são iguais as funções

Mais funções: Aleph 11 - Volume 2 Pág. 118 Ex. 8

Enunciado

Verifique se são iguais os seguintes pares de funções reais de variável real:

  1. \[\begin{array}{*{20}{l}}
    {f\left( x \right) = \frac{{2 – x}}{{{x^2} – 4}}}&{\text{e}}&{g\left( x \right) = \frac{{ – 1}}{{x + 2}}}
    \end{array}\]
  2. \[\begin{array}{*{20}{l}}
    {f\left( x \right) = \frac{x}{{x – 1}}}&{\text{e}}&{g\left( x \right) = \frac{{{x^2} – x}}{{{{\left( {x – 1} \right)}^2}}}}
    \end{array}\]
  3. \[\begin{array}{*{20}{l}}
    {f\left( x \right) = \frac{{{x^4} – 25}}{{{x^2} + 5}}}&{\text{e}}&{g\left( x \right) = {x^2} – 5}
    \end{array}\]

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções definidas por ramos

A continuidade da função

Mais funções: Aleph 11 - Volume 2 Pág. 116 Ex. 7

Enunciado

Com a ajuda da calculadora gráfica, estude a continuidade das seguintes funções de acordo com os valores que o parâmetro real $m$ toma.

\[\begin{array}{*{20}{c}}
{h\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{m}{x}}& \Leftarrow &{0 < x \leqslant 2} \\
{ – {x^2} + 10x + 3}& \Leftarrow &{x > 2}
\end{array}} \right.}&{}&{\text{e}}&{}&{p\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{3}{x}}& \Leftarrow &{0 < x \leqslant 1} \\
{1 + mx}& \Leftarrow &{x > 1}
\end{array}} \right.}
\end{array}\]

Resolução >> Resolução… Ler mais

0

Aplicando / 11.º Ano / Funções definidas por ramos

Defina a função por ramos

Mais funções: Aleph 11 - Volume 2 Pág. 116 Ex. 6

Enunciado

Considere uma função $f$, real de variável real, de domínio $\mathbb{R}$, cuja representação gráfica se apresenta ao lado.

  1. Complete a tabela:
    $x$
    $f\left( x \right)$ $0$ $1$ $3$ $5$
  2. Determine a equação reduzida de cada uma das retas: AB, BC e CD.
  3. Defina a função $f$ por ramos.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções definidas por ramos

Defina sem usar o símbolo de módulo

Mais funções: Aleph 11 - Volume 2 Pág. 116 Ex. 5

Enunciado

Defina, sem usar o símbolo de módulo, e represente graficamente, cada uma das seguintes funções:

  1. $f(x) = \left| {x – 1} \right| + 2$
  2. $g(x) =  – \left| {3{x^2} – 2x – 1} \right|$
  3. $h(x) =  – \left| {x\left( {x – 2} \right)\left( {x + 1} \right)} \right|$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Derivadas / Aplicando / 11.º Ano

Uma bola desce um plano inclinado

Funções racionais: Aleph 11 - Volume 2 Pág. 64 Ex. 5

Enunciado

Uma bola desce um plano inclinado, onde foi espalhado um gel que dificulta o movimento.

A distância, $d$, em centímetros, da bola ao topo do plano inclinado em função do tempo, $t$, em segundos, é dada por: \[d\left( t \right) = 1,3{t^2} – t + 2\]

  1. Represente graficamente a função $d$ na situação descrita.
  2. Determine a velocidade média da bola no 1.º segundo de movimento.
  3. Determine a velocidade da bola no instante $t = 2$ s.
  4. Determine
… Ler mais
0

Aplicando / 11.º Ano / Funções racionais

Concentração do composto

Funções racionais: Aleph 11 - Volume 2 Pág. 53 Ex. 1

Enunciado

Juntou-se ácido puro a $30$ gramas de uma substância $30$% ácida.

Seja $x$ o número de gramas de ácido puro adicionado.

  1. Determine uma expressão que represente a concentração do composto formado.
  2. Represente graficamente a função da alínea anterior.
  3. Entre que valores varia a função?
  4. Qual a quantidade de ácido puro que devemos adicionar para produzir uma solução $75$% ácida?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções racionais

Determine o conjunto solução de cada uma das condições

Funções racionais: Aleph 11 - Volume 2 Pág. 52 Ex. 12

Enunciado

Considere a função $f$ definida por: \[f\left( x \right) = \frac{x}{{{x^2} – 3x + 2}}\]

Determine o conjunto solução de cada uma das inequações:

  1. $f\left( x \right) > 0$
  2. $f\left( {x – 2} \right) > 0$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções racionais

Considera a função $g\left( x \right) = \frac{1}{x}$

Funções racionais: Aleph 11 - Volume 2 Pág. 52 Ex. 10

Enunciado

Considera a função $g\left( x \right) = \frac{1}{x}$, de domínio $\mathbb{R}\backslash \left\{ 0 \right\}$.

  1. Que transformações geométricas se devem efetuar a partir do gráfico de $g$ para se obter o gráfico da função \[f\left( x \right) = \frac{{x – 1}}{{2x – 3}}\] de domínio $\mathbb{R}\backslash \left\{ {\frac{3}{2}} \right\}$, representada graficamente ao lado.
  2. Quais as assíntotas do gráfico da função $f$?
  3. Determina o contradomínio de $f$.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções racionais

Três funções

Funções racionais: Aleph 11 - Volume 2 Pág. 51 Ex. 9

Enunciado

  1. Represente graficamente, no mesmo referencial, as seguintes funções:
    \[\begin{array}{*{20}{r}}
    {f\left( x \right) = x + 1}&{\text{;}}&{g\left( x \right) = f\left( {\frac{1}{x}} \right)}&{\text{e}}&{h\left( x \right) = \frac{1}{{f\left( x \right)}}}
    \end{array}\]
  2. Determine o domínio de cada uma das funções anteriores.
  3. Compare os três gráficos.
    Quais os pontos dos gráficos de $g$ e de $h$ que se mantêm invariantes relativamente ao gráfico de $f$?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções racionais

Determine as assíntotas do gráfico das seguintes funções

Funções racionais: Aleph 11 - Volume 2 Pág. 51 Ex. 8

Enunciado

Determine as assíntotas do gráfico de cada uma das seguintes funções:

\[\begin{array}{*{20}{c}}
{f\left( x \right) = \frac{{2x – 1}}{{x + 3}}}&{\text{e}}&{g\left( x \right) = \frac{{2{x^2} – 7x + 3}}{{x – 3}}}
\end{array}\]

Resolução >> Resolução

<< Enunciado… Ler mais
0

11.º Ano / Funções racionais / Aplicando

Uma peça de forma cilíndrica

Funções racionais: Aleph 11 - Volume 2 Pág. 51 Ex. 6

Enunciado

Uma empresa de alumínio pretende fabricar uma peça de forma cilíndrica, com capacidade de $500$ cm3.

As tampas superior e inferior são feitas de alumínio especial que custa $5$ cêntimos por centímetro quadrado.

A superfície lateral é feita de material mais barato, que custa $2$ cêntimos por centímetro quadrado.

  1. Exprima o custo $C$ da peça em função do raio $r$ da base.
  2. Faça uma representação gráfica da função $C$.
  3. Qual é o de $r$ para
… Ler mais