Considera a função $g\left( x \right) = \frac{1}{x}$
Funções racionais: Aleph 11 - Volume 2 Pág. 52 Ex. 10
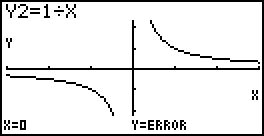
Considera a função $g\left( x \right) = \frac{1}{x}$, de domínio $\mathbb{R}\backslash \left\{ 0 \right\}$.
- Que transformações geométricas se devem efetuar a partir do gráfico de $g$ para se obter o gráfico da função \[f\left( x \right) = \frac{{x – 1}}{{2x – 3}}\] de domínio $\mathbb{R}\backslash \left\{ {\frac{3}{2}} \right\}$, representada graficamente ao lado.
- Quais as assíntotas do gráfico da função $f$?
- Determina o contradomínio de $f$.
- Comecemos por escrever $f(x)$ na forma $a + \frac{b}{{x – c}}$: \[f(x) = \frac{{x – 1}}{{2x – 3}} = \frac{1}{2} \times \frac{{x – 1}}{{x – \tfrac{3}{2}}} = \frac{1}{2} \times \frac{{x – \tfrac{3}{2} + \tfrac{1}{2}}}{{x – \tfrac{3}{2}}} = \frac{1}{2} \times \left( {1 + \frac{{\tfrac{1}{2}}}{{x – \tfrac{3}{2}}}} \right) = \frac{1}{2} + \frac{{\tfrac{1}{4}}}{{x – \tfrac{3}{2}}}\]
O gráfico de $f$ pode ser obtido do gráfico de $g$ através da seguinte sequência de transformações:
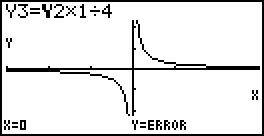
– obtenção do gráfico de $p$, por contração do gráfico de $g$ em relação ao eixo Oy com fator $\frac{1}{4}$;
– obtenção do gráfico de $q$ por translação do gráfico de $p$, associada ao vetor de coordenadas$\left( {\frac{3}{2},0} \right)$;
– finalmente, obtenção do gráfico de $f$ por translação do gráfico de $q$, associada ao vetor de coordenadas $\left( {0,\frac{1}{2}} \right)$.
Gráfico de $g$, sendo $g\left( x \right) = \frac{1}{x}$. Gráfico de $p$, sendo $p(x) = \frac{1}{4}g\left( x \right)$. Gráfico de $q$,
sendo $q\left( x \right) = p\left( {x – \frac{3}{2}} \right) = \frac{1}{4}g\left( {x – \frac{3}{2}} \right)$.\[\begin{array}{*{20}{c}}
{ \leftarrow \frac{1}{4}g\left( {x – \frac{3}{2}} \right) + \frac{1}{2} = f\left( x \right) = \frac{{x – 1}}{{2x – 3}} \to }
\end{array}\]Gráfico de $f$,
sendo $f\left( x \right) = q\left( x \right) + \frac{1}{2} = \frac{1}{4}g\left( {x – \frac{3}{2}} \right) + \frac{1}{2}$.Gráfico de $f$,
sendo $f\left( x \right) = \frac{{x – 1}}{{2x – 3}} = \frac{1}{2} + \frac{{\tfrac{1}{4}}}{{x – \tfrac{3}{2}}}$. - Como se sabe, o gráfico de $g$ admite uma assíntota vertical, de equação $x = 0$, e uma assíntota horizontal, de equação $y = 0$.
O gráfico de $p$ ($p(x) = \frac{1}{4}g\left( x \right)$) admite as mesmas assíntotas do gráfico de $g$, pois a contração do gráfico de $g$ em relação ao eixo Oy com fator $\frac{1}{4}$ não altera as assíntotas.
Ora, a sequência das duas translações a seguir aplicadas ao gráfico de $p$ para obter o gráfico de $f$ é equivalente à translação associada ao vetor $\overrightarrow u = \left( {\frac{3}{2},\frac{1}{2}} \right)$.
Assim, as assíntotas do gráfico de $f$ são as transformadas das assíntotas do gráfico de $g$ pela translação associada ao vetor $\overrightarrow u = \left( {\frac{3}{2},\frac{1}{2}} \right)$, cujas equações são: $x = \frac{1}{2}$ e $y = \frac{3}{2}$.
- Como se sabe, o contradomínio da função $g$ é $D{‘_g} = \mathbb{R}\backslash \left\{ 0 \right\}$.
Como $p(x) = \frac{1}{4}g\left( x \right)$, então o contradomínio de $p$ será $D{‘_p} = D{‘_g} = \mathbb{R}\backslash \left\{ 0 \right\}$, pois, para o mesmo objeto, a imagem por $p$ será $\frac{1}{4}$ da imagem por $g$.
Finalmente, como o gráfico de $f$ se obtém do gráfico de $p$ por uma translação associada ao vetor $\overrightarrow u = \left( {\frac{3}{2},\frac{1}{2}} \right)$, resulta que $D{‘_f} = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}$.
