Três funções
Funções racionais: Aleph 11 - Volume 2 Pág. 51 Ex. 9
Enunciado
- Represente graficamente, no mesmo referencial, as seguintes funções:
\[\begin{array}{*{20}{r}}
{f\left( x \right) = x + 1}&{\text{;}}&{g\left( x \right) = f\left( {\frac{1}{x}} \right)}&{\text{e}}&{h\left( x \right) = \frac{1}{{f\left( x \right)}}}
\end{array}\] - Determine o domínio de cada uma das funções anteriores.
- Compare os três gráficos.
Quais os pontos dos gráficos de $g$ e de $h$ que se mantêm invariantes relativamente ao gráfico de $f$?
Resolução
- \[\begin{array}{*{20}{r}}
{f\left( x \right) = x + 1}&{\text{;}}&{g\left( x \right) = f\left( {\frac{1}{x}} \right) = \frac{1}{x} + 1}&{\text{e}}&{h\left( x \right) = \frac{1}{{f\left( x \right)}} = \frac{1}{{x + 1}}}
\end{array}\]
Representação gráfica das funções $f$, $g$ e $h$
- \[{D_f} = \left\{ {x \in \mathbb{R}:\left( {x + 1} \right) \in \mathbb{R}} \right\} = \mathbb{R}\]
\[{D_g} = \left\{ {x \in \mathbb{R}:\left( {\frac{1}{x} + 1} \right) \in \mathbb{R}} \right\} = \left\{ {x \in \mathbb{R}:x \ne 0} \right\} = \mathbb{R}\backslash \left\{ 0 \right\}\]
\[{D_h} = \left\{ {x \in \mathbb{R}:\left( {\frac{1}{{x + 1}}} \right) \in \mathbb{R}} \right\} = \left\{ {x \in \mathbb{R}:x + 1 \ne 0} \right\} = \mathbb{R}\backslash \left\{ { – 1} \right\}\]
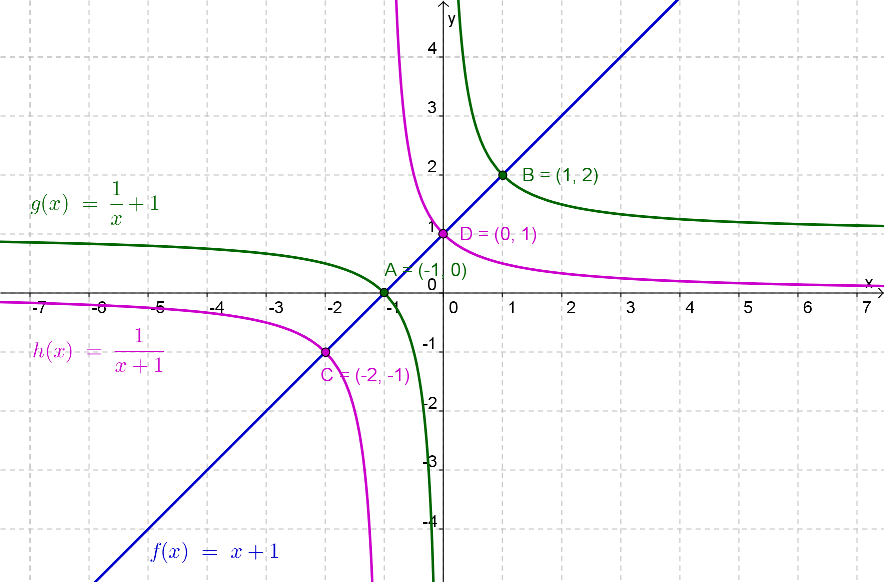
- Os pontos $A\left( { – 1,0} \right)$ e $B\left( {1,2} \right)$, do gráfico de $g$, são invariantes relativamente ao gráfico de $f$.
Os pontos $C\left( { – 2, – 1} \right)$ e $D\left( {0,1} \right)$, do gráfico de $h$, são invariantes relativamente ao gráfico de $f$.
