Concentração do composto

Funções racionais: Aleph 11 - Volume 2 Pág. 53 Ex. 1

by AMMA · Published 8 de Fevereiro de 2014 · Updated 22 de Janeiro de 2022

Enunciado

Juntou-se ácido puro a $30$ gramas de uma substância $30$% ácida.

Seja $x$ o número de gramas de ácido puro adicionado.

Determine uma expressão que represente a concentração do composto formado.
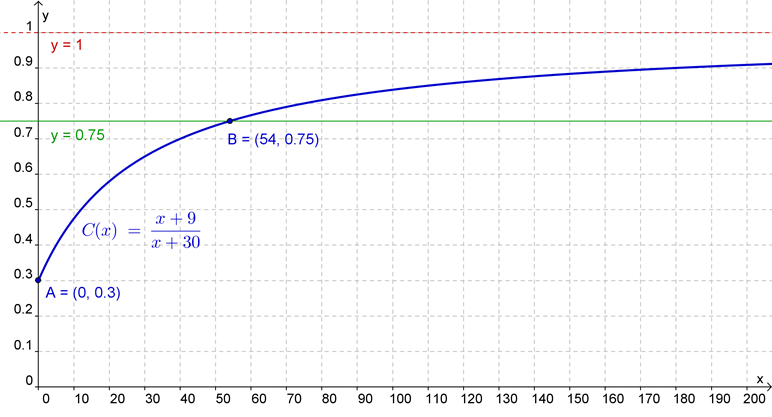
Represente graficamente a função da alínea anterior.
Entre que valores varia a função?
Qual a quantidade de ácido puro que devemos adicionar para produzir uma solução $75$% ácida?

Resolução

Massa de ácido (em gramas): $x + 30\% \times 30 = x + 9$.
Massa do composto (em gramas): $x + 30$.

Portanto, a concentração do composto formado pode ser expressa por: \[C\left( x \right) = \frac{{x + 9}}{{x + 30}}\]
Se considerarmos que não há qualquer limitação quanto à quantidade de ácido possível de adicionar, o domínio da função é $\mathbb{R}_0^ + $.
Por outro lado, como \[C\left( x \right) = \frac{{x + 9}}{{x + 30}} = \frac{{x + 30 – 21}}{{x + 30}} = 1 + \frac{{ – 21}}{{x + 30}}\] o gráfico da função admite uma assíntota horizontal de equação $y = 1$, quando $x \to + \infty $.

A função está representada graficamente na figura abaixo.
$C\left( 0 \right) = \frac{{0 + 9}}{{0 + 30}} = \frac{3}{{10}}$.
Por outro lado, como a função é contínua, estritamente crescente e \[\mathop {\lim }\limits_{x \to + \infty } C\left( x \right) = {1^ – }\] então o contradomínio da função é $\left[ {\frac{3}{{10}},1} \right[$.

Logo, a função assume todos os valores do intervalo $\left[ {\frac{3}{{10}},1} \right[$.
Tem-se sucessivamente:
\[\begin{array}{*{20}{l}}
{C\left( x \right) = 0,75}& \Leftrightarrow &{\frac{{x + 9}}{{\mathop {x + 30}\limits_{\left( 4 \right)} }} – \mathop {\frac{3}{4}}\limits_{\left( {x + 30} \right)} = 0} \\
{}& \Leftrightarrow &{\frac{{4x + 36 – 3x – 90}}{{4x + 120}} = 0} \\
{}& \Leftrightarrow &{\frac{{x – 54}}{{4x + 120}} = 0} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x – 54 = 0}& \wedge &{4x + 120 \ne 0}
\end{array}} \\
{}& \Leftrightarrow &{x = 54}
\end{array}\]

Portanto, para produzir uma solução $75$% ácida, devemos adicionar $54$ gramas de ácido puro.