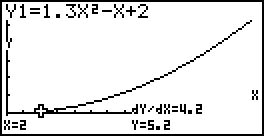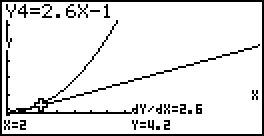Uma bola desce um plano inclinado
Funções racionais: Aleph 11 - Volume 2 Pág. 64 Ex. 5
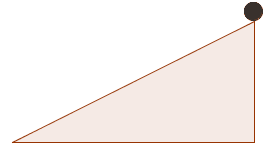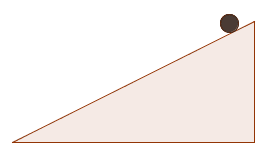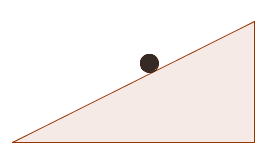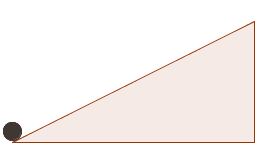 Uma bola desce um plano inclinado, onde foi espalhado um gel que dificulta o movimento.
Uma bola desce um plano inclinado, onde foi espalhado um gel que dificulta o movimento.
A distância, $d$, em centímetros, da bola ao topo do plano inclinado em função do tempo, $t$, em segundos, é dada por: \[d\left( t \right) = 1,3{t^2} – t + 2\]
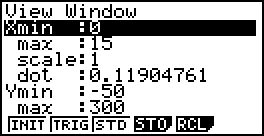
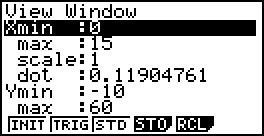
- Represente graficamente a função $d$ na situação descrita.
- Determine a velocidade média da bola no 1.º segundo de movimento.
- Determine a velocidade da bola no instante $t = 2$ s.
- Determine o instante em que a bola tem uma velocidade de $30$ cm/s.
- Construa o gráfico da velocidade da bola em função do tempo.
- Admite-se que a bola demora $15$ segundos a descer o plano inclinado.
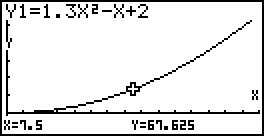
Apresenta-se seguidamente uma representação gráfica da função $d$:


Note que o modelo considerado não é
estritamente crescente em $\mathbb{R}_0^ + $. - \[tm{v_{\left[ {0,1} \right]}} = \frac{{d\left( 1 \right) – d\left( 0 \right)}}{{1 – 0}} = \frac{{\left( {1,3 \times {1^2} – 1 + 2} \right) – 2}}{1} = 0,3\]
No 1.º segundo de movimento, a bola desceu o plano inclinado com velocidade média $0,3$ cm/s. - Para ${h > 0}$, vem:
\[\begin{array}{*{20}{l}}
{\mathop {tm{v_{\left[ {2,2 + h} \right]}}}\limits_{h > 0} }& = &{\frac{{1,3{{\left( {2 + h} \right)}^2} – \left( {2 + h} \right) + 2 – \left( {1,3 \times {2^2} – 2 + 2} \right)}}{{2 + h – 2}}} \\
{}& = &{\frac{{1,3 \times {2^2} + 1,3 \times 4h + 1,3{h^2} – 2 – h + 2 – 1,3 \times {2^2}}}{h}} \\
{}& = &{\frac{{1,3{h^2} + 4,2h}}{h}} \\
{}& = &{1,3h + 4,2}
\end{array}\]Para ${h < 0}$, vem:
\[\begin{array}{*{20}{l}}
{\mathop {tm{v_{\left[ {2 + h,2} \right]}}}\limits_{h < 0} }& = &{\frac{{\left( {1,3 \times {2^2} – 2 + 2} \right) – \left[ {1,3{{\left( {2 + h} \right)}^2} – \left( {2 + h} \right) + 2} \right]}}{{2 – h – 2}}} \\
{}& = &{\frac{{ – 1,3{h^2} – 4,2h}}{{ – h}}} \\
{}& = &{1,3h + 4,2}
\end{array}\]Ora, se $h \to {0^ + }$, então $\mathop {tm{v_{\left[ {2,2 + h} \right]}}}\limits_{h > 0} = 1,3h + 4,2 \to 4,2$ e se $h \to {0^ – }$, então $\mathop {tm{v_{\left[ {2 + h,2} \right]}}}\limits_{h < 0} = 1,3h + 4,2 \to 4,2$.
 Portanto, a taxa de variação da função $d$, para $t = 2$ é $4,2$.
Portanto, a taxa de variação da função $d$, para $t = 2$ é $4,2$.Assim, no instante $t = 2$ s a velocidade da bola é $4,2$ cm/s.
Também se pode obter esse valor na calculadora gráfica, ativando a opção “Derivative”, conforme se ilustra na imagem ao lado.
- Seja ${t_0} \in {D_d}$ e calculemos $d’\left( {{t_0}} \right)$:
\[\begin{array}{*{20}{l}}
{d’\left( {{t_0}} \right)}& = &{\mathop {\lim }\limits_{t \to 0} \frac{{d\left( {{t_0} + h} \right) – d\left( {{t_0}} \right)}}{h}} \\
{}& = &{\mathop {\lim }\limits_{t \to 0} \frac{{1,3{{\left( {{t_0} + h} \right)}^2} – \left( {{t_0} + h} \right) + 2 – \left( {1,3 \times {t_0}^2 – {t_0} + 2} \right)}}{h}} \\
{}& = &{\mathop {\lim }\limits_{t \to 0} \frac{{1,3{t_0}^2 + 2,6{t_0} \times h + 1,3{h^2} – {t_0} – h + 2 – 1,3 \times {t_0}^2 + {t_0} – 2}}{h}} \\
{}& = &{\mathop {\lim }\limits_{t \to 0} \frac{{2,6{t_0} \times h + 1,3{h^2} – h}}{h}} \\
{}& = &{\mathop {\lim }\limits_{t \to 0} \left( {2,6{t_0} + 1,3h – 1} \right)} \\
{}& = &{2,6{t_0} – 1}
\end{array}\]Como
\[\begin{array}{*{20}{l}}
{d’\left( {{t_0}} \right) = 30}& \Leftrightarrow &{2,6{t_0} – 1 = 30} \\
{}& \Leftrightarrow &{{t_0} = \frac{{31}}{{2,6}}} \\
{}& \Leftrightarrow &{{t_0} = \frac{{155}}{{13}}} \\
{}&{}&{{t_0} = 11,92}
\end{array}\]
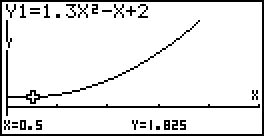
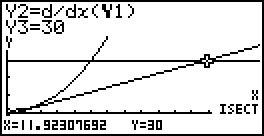
então a bola tem uma velocidade de $30$ cm/s no instante $t = 11,9$ s, aproximadamente.Também se pode obter um valor aproximado desse instante recorrendo à calculadora gráfica:



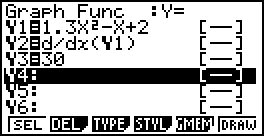
- Como se determinou, na alínea anterior, a expressão de ${d’\left( t \right)}$, pode construir-se o gráfico da velocidade da bola em função do tempo:
Na aplicação seguinte, pode fazer a exploração da resolução gráfica do problema: