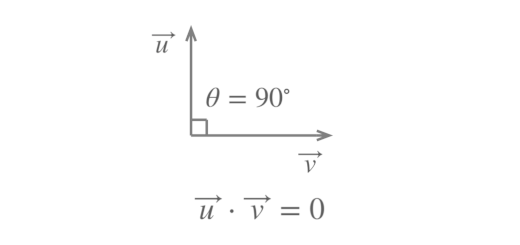Tagged: Geometria

• Enunciado
• Resolução

Averigue se são ou não perpendiculares as retas r e s de equações:

1. r: $y=2x-3$ e s: $y=-x+\frac{1}{2}$;
2. r: $x=3$ e s: $y=4$;
3. r: $2x+3y-1=0$ e s: $3x-2y+7=0$.

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j})$ um referencial o.n. do plano.

1. Escreva uma equação da reta que passa no ponto $A(2,3)$ e é perpendicular a $\vec{u}(-1,4)$ .
2. Escreva uma equação da reta que passa em $B(-3,4)$ e é perpendicular à recta de equação $2x-5y+1=0$.
3. Sejam $A(2,1)$ e $B(1,5)$ dois pontos do plano.
   Determine uma equação da mediatriz de [AB].

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j},\vec{k})$ um referencial o. n. do espaço.

1. Calcule a amplitude do ângulo formado pela diagonal de um cubo com qualquer das suas arestas.
2. O vetor ${\vec{u}}$  é tal que $\vec{u}=2\vec{i}+2\vec{j}+2\vec{k}$.
   Indique, em radianos, uma medida de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{i})$, de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{j})$ e de $(\vec{u}\overset{\hat{\ }}{\mathop{{}}}\,\vec{k})$.

Resolução >> Resolução

• Enunciado
• Resolução

Seja $(O,\vec{i},\vec{j})$ um referencial o. n. do plano.

Determine o ângulo que a reta r faz com a reta s:

1. r: $(x,y)=(1,3)+k.(-2,-2)\,,\,\,k\in \mathbb{R}$ e s: $3y-x-2=0$;
2. r: $x+2y+5=0$ e s: $y=\frac{3}{4}x-3$.

Resolução >> Resolução

• Enunciado
• Resolução

Averigue se o triângulo [ABC] é triângulo retângulo e isósceles, sendo:

1. $A(1,1,\sqrt{2})$, $B(\sqrt{2},-\sqrt{2},0)$ e C o simétrico de A em relação a O, origem do referencial;
2. $A(2,1,-3)$, $B(-1,3,4)$ e $C(-3,0,2)$.

Resolução >> Resolução

• Enunciado
• Resolução

Averigue se os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ são perpendiculares:

1. $\vec{u}(1,-3,2)$  e $\vec{v}(2,4,5)$
2. $\vec{u}(\sqrt{3}-1,4,-1)$  e $\vec{v}(\sqrt{3}+1,1,6)$
3. $\vec{u}(\frac{2}{3},-\frac{3}{2},\frac{5}{7})$  e $\vec{v}(-\frac{3}{2},\frac{2}{3},\frac{7}{5})$
4. $\vec{u}(-5,\alpha ,3)$  e  $\vec{v}(2\alpha ,10,0)$

Resolução >> Resolução

• Enunciado
• Resolução

Supondo que $\overrightarrow{u}\bot \overrightarrow{w}$ e $\overrightarrow{u}.\overrightarrow{v}=2\sqrt{5}$, calcule, aplicando as propriedades do produto escalar:

1. $(2\vec{u}).(3\vec{v})$
2. $\vec{u}.(4\vec{v}-2\vec{w})$

Resolução >> Resolução

• Enunciado
• Resolução

Determine (se necessário apresente o resultado aproximado às décimas) a amplitude do ângulo de $\overrightarrow{u}$ com $\overrightarrow{v}$, sabendo que:

1. $\overrightarrow{u}.\overrightarrow{v}=50\sqrt{2}$ e $\left\| \overrightarrow{u} \right\|=\left\| \overrightarrow{v} \right\|=10$
2. $\overrightarrow{u}.\overrightarrow{v}=-10\sqrt{3}$ e $\left\| \overrightarrow{u} \right\|=4$ e $\left\| \overrightarrow{v} \right\|=5$
3. $\overrightarrow{u}(1,2,3)$ e $\overrightarrow{v}(-1,1,-1)$
4. $\overrightarrow{u}(\frac{2}{3},\frac{2}{3},1)$ e $\overrightarrow{v}(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},0)$

Resolução >> Resolução

• Enunciado
• Resolução

Sendo $\overrightarrow{u}$ e $\overrightarrow{v}$ dois vetores, tais que $\left\| \overrightarrow{u} \right\|=2$, $\left\| \overrightarrow{v} \right\|=3$ e $\overrightarrow{u}.\overrightarrow{v}=4$, calcule:

1. $(2\overrightarrow{u}-\overrightarrow{v}).(\overrightarrow{u}+\overrightarrow{v})$
2. ${{(2\overrightarrow{u}+5\overrightarrow{v})}^{2}}$

Resolução >> Resolução

• Enunciado
• Resolução

[ABCDE] é um pentágono regular de lado l, inscrito na circunferência de centro O e raio r.

1. Calcule em função de r, com aproximação às centésimas:

   $\overrightarrow{OA}.\overrightarrow{OB}$, $\overrightarrow{OA}.\overrightarrow{OE}$ e $\overrightarrow{OA}.\overrightarrow{OC}$.

2. Determine, em função de l, com aproximação às centésimas:

   $\overrightarrow{AB}.\overrightarrow{AE}$, $\overrightarrow{AB}.\overrightarrow{ED}$, $\overrightarrow{AB}.\overrightarrow{AD}$ e $\overrightarrow{AB}.\overrightarrow{AC}$.

Resolução >> Resolução

• Enunciado
• Resolução

Os vetores $\overrightarrow{u}$ e $\overrightarrow{v}$ verificam a condições, em $(O,\overrightarrow{i},\overrightarrow{j})$:

• $\begin{matrix}
  \overrightarrow{u}.\overrightarrow{i}=2 & \wedge  & \overrightarrow{u}.\overrightarrow{j}=-3  \\
  \end{matrix}$
• $\begin{matrix}
  \overrightarrow{v}.\overrightarrow{i}=-4 & \wedge  & \overrightarrow{v}.\overrightarrow{j}=-5  \\
  \end{matrix}$

1. Quais são as coordenadas de $\overrightarrow{u}$ e de $\overrightarrow{v}$?
2. Calcule $\overrightarrow{u}.\overrightarrow{v}$.

Resolução >> Resolução

• Enunciado
• Resolução

Considere os vetores $\vec{u}(-3,1,2)$, $\vec{v}(4,-2,5)$ e $\vec{w}(2,3,-1)$.

1. Calcule os números reais a e b, para que o vetor $\vec{v}-\vec{w}$ e o vetor $(a,b,3-a)$ sejam colineares.
2. Calcule os números reais $\alpha $ e $\beta $, para que o vetor $\alpha \vec{u}+\beta \vec{v}$ seja igual ao vetor de coordenadas $(-10,4,-1)$.

Resolução >> Resolução

• Enunciado
• Resolução

Considere os vetores $\vec{u}(2,-1,3)$  e $\vec{v}(-4,2,5)$.

1. Os vetores ${\vec{u}}$  e ${\vec{v}}$  são colineares? Porquê?
2. Determine os números reais a e b, para que o vetor $\vec{w}(a,-6,b)$  e o vetor ${\vec{v}}$  sejam colineares.

Resolução >> Resolução

• Enunciado
• Resolução

Considere um referencial ortonormado $(O,\vec{i},\vec{j},\vec{k})$.

Dados os pontos $A\,(-2,1,5)$, $B\,(1,-3,0)$ e $C\,(2,2,-1)$

1. Determine as coordenadas do ponto M, tal que $\overrightarrow{BM}=3\,\overrightarrow{AB}+2\,\overrightarrow{AC}$.
2. Determine as coordenadas do ponto N, tal que $2\,\overrightarrow{NA}=3\,\overrightarrow{NB}$.
3. Calcule as coordenadas do ponto médio I de [MN].
4. Calcule as coordenadas do simétrico de C em relação a I.

Resolução >> Resolução