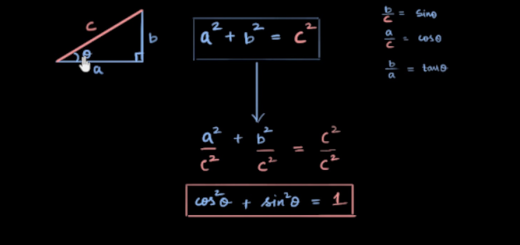
A Casinha da Matemática

• Enunciado
• Resolução

Enunciado

Com a ajuda da calculadora e de um círculo trigonométrico, determine $\theta $ (em radianos), tal que:

1. $\begin{matrix}
   sen\,\theta =\frac{2}{3} & \wedge  & \frac{\pi }{2}<\theta <\pi   \\
   \end{matrix}$
2. $\begin{matrix}
   sen\,\theta =-\frac{1}{3} & \wedge  & \pi <\theta <\frac{3\pi }{2}  \\
   \end{matrix}$
3. $\begin{matrix}
   tg\,\theta =\frac{7}{3} & \wedge  & \pi <\theta <\frac{3\pi }{2}  \\
   \end{matrix}$
4. $\begin{matrix}
   \cos \theta =\frac{2}{5} & \wedge  & \frac{3\pi }{2}<\theta <2\pi   \\
   \end{matrix}$
5. $\begin{matrix}
   tg\,\theta =-9 & \wedge  & \frac{\pi }{2}<\theta <\pi   \\
   \end{matrix}$

(Apresente o … Ler mais

• Enunciado
• Resolução

Enunciado

Na figura está representado um círculo trigonométrico.

O segmento [OA] é perpendicular a [OB]. O ângulo COB tem amplitude $\alpha $ radianos.

1. Calcule as coordenadas do ponto A.
2. Determine o valor exato da expressão: $tg\,(\pi -\alpha )+\cos (\pi +\alpha )$.

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Tendo em atenção a variação do seno e do cosseno, compare, se possível, cos a e cos b e sen a e sen b nos seguintes casos:

1. $0\le a\le b\le \frac{\pi }{2}$
2. $\pi \le a\le b\le 2\pi $
3. $\pi \le a\le b\le \frac{3\pi }{2}$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Dos ângulos compreendidos entre $0$ e $2\pi $, indique:

1. os que têm seno simétrico do seno de $\frac{\pi }{8}$
2. os que têm o co-seno igual ao seno de $\frac{\pi }{8}$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Indique uma expressão geral dos ângulos que têm:

1. seno igual a $-0,5$
2. co-seno igual a $0$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Observe a figura onde está representado um triângulo equilátero inscrito numa circunferência de raio 6 unidades. O ponto C pertence ao eixo das ordenadas.

1. Indique as coordenadas dos vértices do triângulo.
2. Indique as coordenadas do ortocentro do triângulo (ponto de intersecção das alturas do triângulo).
3. Se o triângulo rodar 90º em torno de O, quais serão agora as coordenadas dos seus vértices?

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Sabendo que $\cos \frac{\pi }{8}=\frac{1}{2}\sqrt{2+\sqrt{2}}$, calcule o cosseno de:

1. $-\frac{\pi }{8}$
2. $\frac{3\pi }{8}$
3. $\frac{5\pi }{8}$
4. $\frac{9\pi }{8}$
5. $-\frac{325\pi }{8}$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

1. Se $\cos (\alpha -\frac{\pi }{2})=\frac{4}{5}$, calcule o valor numérico de $\begin{matrix}
   \cos (-\alpha )-\cos (\pi +\alpha ) & \wedge  & \alpha \in 1.{}^\text{o}Q  \\
   \end{matrix}$.
2. Determine o valor exato de $tg\,(-\alpha )+\cos (\alpha -\frac{\pi }{2})$, sabendo que $\begin{matrix}
   sen\,(-\pi -\alpha )=\frac{3}{7} & \wedge  & \alpha \in 2.{}^\text{o}Q  \\
   \end{matrix}$.

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Calcule o valor exato de cada uma das expressões.

1. $sen\,\frac{13\pi }{3}+\cos 5\pi -tg\,(-7\pi )+\cos (-\frac{23\pi }{4})$
2. $se{{n}^{2}}\,(-\frac{7\pi }{4})+{{\cos }^{2}}(-\frac{7\pi }{4})$
3. $sen\,\frac{19\pi }{3}+\cos (-3\pi )-tg\,(-\frac{15\pi }{4})+\cos (-\frac{11\pi }{6})$
4. $tg\,\frac{13\pi }{4}+\cos 6\pi -sen\,(-\frac{7\pi }{2})+\cos (-\frac{17\pi }{3})$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Exprima A(x) em função de sen x e cos x.

1. $A(x)=sen\,(-x)-sen\,(\pi -x)$
2. $A(x)=\cos (-x)+\cos (\pi +x)$
3. $A(x)=sen\,(\frac{\pi }{2}-x)+\cos (\frac{5\pi }{2}-x)$
4. $A(x)=\cos (\frac{3\pi }{2}+x)+sen\,(x-\frac{5\pi }{2})$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Recorrendo ao círculo trigonométrico, exprima, em função de sen b e cos b, as expressões:

1. $sen\,(b+\pi )+sen\,(b+2\pi )+sen\,(b-\pi )$
2. $\cos (b+\pi )+sen\,(b+\frac{\pi }{2})+\cos (b-\pi )+sen\,(b+\frac{3\pi }{2})$
3. $sen\,(-b-\pi )-2\cos (-\frac{\pi }{2}-b)+sen\,(-\frac{3\pi }{2}+b)$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado

Trace um círculo trigonométrico e utilize-o para exprimir em função de sen α e de cos α as expressões:

1. $sen\,(\alpha -\pi )$ e $\cos (\alpha -\pi )$
2. $sen\,(-\alpha +\frac{5\pi }{2})$ e $\cos (-\alpha +\frac{5\pi }{2})$
3. $sen\,(-\alpha -5\pi )$ e $\cos (-\alpha -5\pi )$
4. $sen\,(\frac{7\pi }{2}-\alpha )$ e $\cos (\frac{7\pi }{2}-\alpha )$
5. $sen\,(-\alpha +10\pi )$ e $\cos (-\alpha +10\pi )$

Resolução >> Resolução

<< Enunciado… Ler mais

• Enunciado
• Resolução

Enunciado Sabe-se que $sen\,(\alpha +\pi )=a$.

1. Determine, em função de a, $sen\,(2\pi -\alpha )$.
2. Determine os valores de $\alpha $ $(0<\alpha <2\pi )$, quando $a=0,5$.
3. Se o ângulo $\alpha $ estiver compreendido entre $5\frac{\pi }{3}\,rad$ e $3\frac{\pi }{2}\,rad$, quem é maior: o seu seno o o seu cosseno?

Resolução >> Resolução

<< Enunciado… Ler mais