Sabe-se que…
Trigonometria: Infinito 11 A - Parte 1 Pág. 95 Ex. 50
Enunciado Sabe-se que $sen\,(\alpha +\pi )=a$.
- Determine, em função de a, $sen\,(2\pi -\alpha )$.
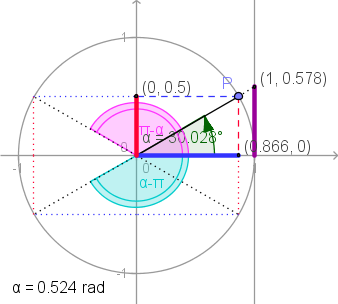
- Determine os valores de $\alpha $ $(0<\alpha <2\pi )$, quando $a=0,5$.
- Se o ângulo $\alpha $ estiver compreendido entre $5\frac{\pi }{3}\,rad$ e $3\frac{\pi }{2}\,rad$, quem é maior: o seu seno o o seu cosseno?
Resolução
- Como $sen\,(\alpha +\pi )=a\Leftrightarrow sen\,\alpha =-a$, então $sen\,(2\pi -\alpha )=sen\,(-\alpha )=-sen\,\alpha =a$.
- Para $a=0,5$, temos \[\begin{array}{*{35}{l}} \begin{matrix} sen\,\alpha =-\frac{1}{2} & \wedge & 0<\alpha <2\pi \\ \end{matrix} & \Leftrightarrow & \begin{matrix} \alpha =\frac{\pi }{6}+\pi & \vee & \alpha =2\pi -\frac{\pi }{6} \\ \end{matrix} \\ {} & \Leftrightarrow & \begin{matrix} \alpha =\frac{7\pi }{6} & \vee & \alpha =\frac{11\pi }{6} \\ \end{matrix} \\ \end{array}\] (Conclua as soluções no círculo trigonométrico)

- Se $\alpha \in \left] 3\frac{\pi }{2},5\frac{\pi }{3} \right[$, então $sen\,\alpha <0$ e $\cos \alpha >0$.
Logo é maior o seu cosseno.