Exprime em função de sen α e de cos α
Trigonometria: Infinito 11 A - Parte 1 Pág. 96 Ex. 51
Enunciado
Trace um círculo trigonométrico e utilize-o para exprimir em função de sen α e de cos α as expressões:
- $sen\,(\alpha -\pi )$ e $\cos (\alpha -\pi )$
- $sen\,(-\alpha +\frac{5\pi }{2})$ e $\cos (-\alpha +\frac{5\pi }{2})$
- $sen\,(-\alpha -5\pi )$ e $\cos (-\alpha -5\pi )$
- $sen\,(\frac{7\pi }{2}-\alpha )$ e $\cos (\frac{7\pi }{2}-\alpha )$
- $sen\,(-\alpha +10\pi )$ e $\cos (-\alpha +10\pi )$
Resolução
- $sen\,(\alpha -\pi )=-sen\,(\pi -\alpha )=-sen\,\alpha $
$\cos (\alpha -\pi )=\cos (\pi -\alpha )=-\cos \alpha $
- $sen\,(-\alpha +\frac{5\pi }{2})=sen\,(2\pi +\frac{\pi }{2}-\alpha )=sen\,(\frac{\pi }{2}-\alpha )=\cos \alpha $
$\cos (-\alpha +\frac{5\pi }{2})=\cos (2\pi +\frac{\pi }{2}-\alpha )=\cos (\frac{\pi }{2}-\alpha )=sen\,\alpha $
- $sen\,(-\alpha -5\pi )=sen\,(6\pi -\alpha -5\pi )=sen\,(\pi -\alpha )=sen\,\alpha $
$\cos (-\alpha -5\pi )=\cos (6\pi -\alpha -5\pi )=\cos (\pi -\alpha )=-\cos \alpha $
- $sen\,(\frac{7\pi }{2}-\alpha )=sen\,(4\pi -\frac{\pi }{2}-\alpha )=sen\,(-\frac{\pi }{2}-\alpha )=-sen\,(\frac{\pi }{2}+\alpha )=-sen\,(\frac{\pi }{2}-(-\alpha ))=-\cos (-\alpha )=-\cos \alpha $
$\cos (\frac{7\pi }{2}-\alpha )=\cos (4\pi -\frac{\pi }{2}-\alpha )=\cos (-\frac{\pi }{2}-\alpha )=\cos (\frac{\pi }{2}+\alpha )=\cos (\frac{\pi }{2}-(-\alpha ))=sen\,(-\alpha )=-sen\,\alpha $
- $sen\,(-\alpha +10\pi )=sen\,(-\alpha )=-sen\,\alpha $
$\cos (-\alpha +10\pi )=\cos (-\alpha )=\cos \alpha $


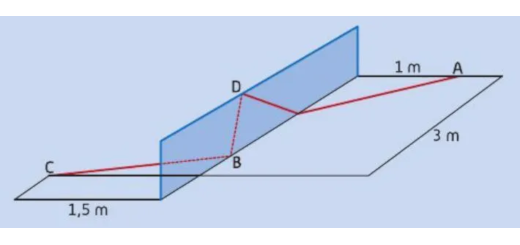












![O perímetro do triângulo [ABC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag60-7a-720x340.png)


