A Casinha da Matemática Blog
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 50 Ex. 23
Enunciado
- Determine as expressões designatórias das funções derivadas das funções:
a) $f:x \to \operatorname{sen} (3x) + \cos x$
b) $g:x \to {\cos ^2}(2x)$
c) $h:\alpha \to \frac{{1 – \cos (3\alpha )}}{\alpha }$
d) $i:z \to \frac{{1 – \cos (2z)}}{{1 + \cos (2z)}}$
e) $j:t \to \cos \left( {4 – 3t} \right)$
- Sabendo que as funções $f$ e $g$ são deriváveis e que $g(1) = 3$, $g'(1) = 2$ e $f'(3) = 5$, determine, nos pontos indicados, o valor
…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 49 Ex. 22
Enunciado
Calcule a derivada de cada uma das funções reais de variável real:
- $f:x \to 3 + 2\cos x$
- $g:x \to \operatorname{sen} x + \cos x$
- $h:t \to \operatorname{sen} t.\cos t$
- $i:z \to 3z\cos z$
- $j:x \to 3x\operatorname{tg} x$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 47 Ex. 19
Enunciado
Determine a expressão designatória da função derivada de cada uma das funções:
- $f:x \to 2\operatorname{sen} x + 5$
- $g:t \to t – 2\operatorname{sen} t$
- $h:\theta \to {\theta ^2}\operatorname{sen} \theta $
Resolução >>
Resolução
<< Enunciado…
Ler mais
9.º Ano: Equação do 2.º grau
A presente Ficha de Trabalho aborda o tema Equação do 2.º grau.
As dificuldades que encontres durante a sua resolução deves tentar superá-las consultando o manual e o caderno diário; depois, poderás tirar as dúvidas na aula ou na sala de estudo.
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 69 Ex. 10
Enunciado
O Sr. José foi contratado para fazer uma calçada à volta de dois lados de um terreno retangular.
O terreno mede 20 metros por 30 metros, como indica a figura, e a calçada deve ter sempre a mesma largura.
Sabendo que o Sr. José dispõe de 72 m2 de lajetas de pavimento para fazer a calçada, que pretende gastar na totalidade, qual deverá ser a largura da calçada?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 69 Ex. 9
Enunciado
De um quadrado de cartão, de lado $x$ centímetros, foi retirado, em cada canto, um quadradinho com 2 centímetros de lado, como mostra a figura.
- Calcula o valor de $x$, sabendo que a figura restante tem área 65 cm2.
- Depois de cortado o cartão, construímos uma caixa aberta.
Determina o valor de $x$ de modo que o volume da caixa seja $50\,c{m^3}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 69 Ex. 8
Enunciado
O Esquilo Kili diz ao Esquilo Kiló:
– Só tenho duas avelãs!
E o Kiló respondeu:
– Metade do quadrado do número das minhas avelãs é igual ao seu quíntuplo. E tenho mais avelãs do que tu!
Quantas avelãs tem o Kiló?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 69 Ex. 5
Enunciado
Qual deve ser o valor de:
- $m$, para que a equação $2{x^2} – 3mx + 2 = 0$ possua apenas uma raiz?
- $n$, para que a equação ${x^2} – 6x + n – 4 = 0$ possua raízes reais?
- $p$, para que a equação $\left( {2p + 1} \right){x^2} – 3x + 1 = 0$ não possua raízes reais?
- $r$, para que a equação ${x^2} – 5x – r – 1 = 0$ tenha duas raízes reais
…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 68 Ex. 3
Enunciado
Resolve as equações:
- ${\sqrt 2 {x^2} + 11x = 0}$
- ${x^2} + 9 = 0$
- $5a + {\left( {a + 2} \right)^2} = 3a\left( {a + 2} \right) + a$
- $4,8{x^2} – 8,4x + 2,4 = 0$
- $\frac{{a – 1}}{2} – \frac{{a\left( {3 – a} \right)}}{3} = a + \frac{1}{3}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 66 Ex. 13
Enunciado
Escreve uma equação do 2.º grau que admita as soluções 1 e 2.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 66 Ex. 12
Enunciado
Escreve uma equação do 2.º grau sabendo que:
- $S = 3$ e $P = 2$;
- $S = – \frac{1}{2}$ e $P = \frac{3}{4}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 65 Ex. 9
Enunciado
Para cada uma das equações determina o binómio discriminante e diz quantas soluções tem:
- ${x^2} – 2x + 1 = 0$
- $2{x^2} – x – 1 = 0$
- ${x^2} + 3x + 4 = 0$
- ${a^2} – 7a – 18 = 0$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 64 Ex. 8
Enunciado
Resolve as seguintes equações usando a fórmula resolvente:
- $2{x^2} + 4x – 4 = 0$
- $6{x^2} + 5x + 1 = 0$
- ${x^2} – 4x + 4 = 0$
- ${x^2} – 3x + 2 = 0$
- ${x^2} – \frac{5}{3}x – \frac{2}{3} = 0$
- $x\left( {x – 8} \right) = – 42 + 5x$
- $4x\left( {2x – 5} \right) = 3x – 14$
- $\frac{x}{4} – \frac{{{{\left( {x – 1} \right)}^2}}}{2} = 0$
- $5\left( {3 + x} \right) =
…
Ler mais
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 61 Ex. 6
Enunciado
Resolve as seguintes equações pelo processo mais adequado:
- ${x^2} – 2x + 1 = 0$
- $9{x^2} + 12x + 4 = 0$
- $4{x^2} – 20x + 25 = 0$
- ${x^2} – 8x = 4$
Resolução >>
Resolução
<< Enunciado…
Ler mais
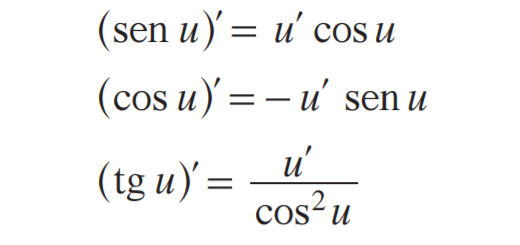






















![Uma corda [BC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag60-2a-720x340.png)




