A Casinha da Matemática

• Enunciado
• Resolução

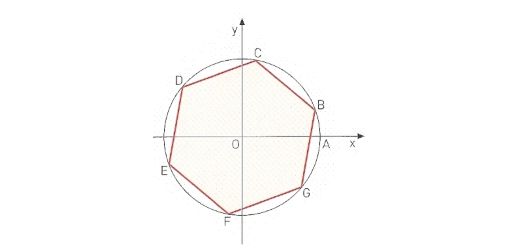
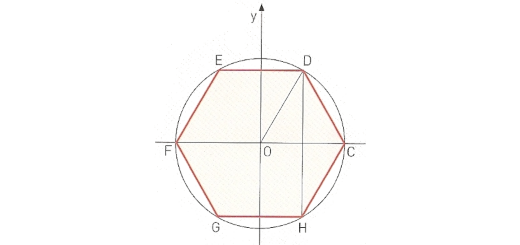
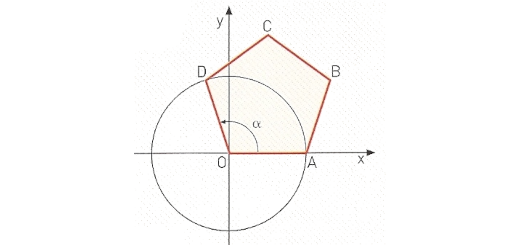
Sobre o círculo trigonométrico de centro O da figura está representado um hexágono regular. A amplitude positiva mínima do ângulo generalizado AOB é $\frac{\pi }{9}$ radianos.

1. Qual é, em radianos, a expressão geral das amplitudes do ângulo AOB?
2. Prove que $\frac{4\pi }{9}$ radianos é uma amplitude do ângulo orientado AOC.
3. Indique, em radianos, a amplitude dos seguintes ângulos generalizados: AOE, AOF e AOG.
4. Determine, com aproximação às décimas, as coordenadas dos pontos E e G.

Resolução >>… Ler mais

• Enunciado
• Resolução

Desenhe no círculo trigonométrico os ângulos seguintes, indicando os valores dos seus senos, cossenos e tangentes.

1. $\frac{7\pi }{3}$
2. $\frac{4\pi }{3}$
3. $\frac{71\pi }{4}$
4. $-\frac{5\pi }{4}$
5. $\frac{23\pi }{6}$
6. $-\frac{425\pi }{6}$
7. $\frac{712\pi }{6}$
8. $-\frac{135\pi }{4}$

Resolução >> Resolução

• Enunciado
• Resolução

Observe a figura ao lado.

Num certo pistão, peça usada em mecânica na transmissão de certos movimentos, a distância x, em metros, do centro do eixo à cabeça do pistão, conforme se assinala na figura, é dado pela fórmula \[x=\cos \theta +\sqrt{16+0,5\cos (2\theta )}\] em que $\theta $ é a amplitude do ângulo representado na figura.

Determine o valor exato de x, quando:

1. $\theta =30{}^\text{o}$;
2. $\theta =45{}^\text{o}$.

Resolução >> Resolução

• Enunciado
• Resolução v1

Observe a figura.

Ignorando o atrito, o tempo t (em segundos) necessário para um bloco deslizar por um plano inclinado é dado pela fórmula \[t=\sqrt{\frac{2a}{g\times sen\,\theta \times \cos \theta }}\]  \[t=\sqrt{\frac{2a}{g\times sen\,\theta }}\] onde a é a medida do comprimento da rampa, em metros, e g é a aceleração da gravidade, aproximadamente 9,8 m/s².

Quanto tempo demora a deslizar um bloco se $a=3,3$ m, quando:

• $\theta =30{}^\text{o}$
• $\theta =45{}^\text{o}$
• $\theta =60{}^\text{o}$

(Aproxime o resultado … Ler mais

• Enunciado
• Resolução

Num referencial cartesiano, está representada uma circunferência com raio de uma unidade de comprimento e um hexágono [CDEFGH].

1. Explique porque é que sabemos que a abcissa de D é $\cos \frac{\pi }{3}$.
2. Determine as coordenadas exactas dos pontos E e G.
3. Qual a medida do comprimento do arco CE na unidade considerada?
4. Se o raio passasse a ter 5 unidades de comprimento, qual era a abcissa de D?

Resolução >> Resolução

• Enunciado
• Resolução

Prove que, para todo o $\theta $, se tem:

1. ${{(sen\,\theta +\cos \theta )}^{2}}=1+2\,sen\,\theta \times \cos \theta $
2. $\cos \theta -se{{n}^{2}}\,\theta \times \cos \theta ={{\cos }^{2}}\theta $
3. $se{{n}^{4}}\,\theta +{{\cos }^{4}}\theta +2\times se{{n}^{2}}\,\theta \times {{\cos }^{2}}\theta =1$
4. ${{(\cos \theta -sen\,\theta )}^{2}}+{{(\cos \theta +sen\,\theta )}^{2}}=2$
5. $(\cos \theta -sen\,\theta )+(\cos \theta +sen\,\theta )-1=-2\times se{{n}^{2}}\,\theta $

Resolução >> Resolução

• Enunciado
• Resolução

1. Sabendo que $tg\,\alpha =\frac{3}{4}$ e $\pi <\alpha <\frac{3\pi }{2}$, determine $sen\,\alpha $ e $\cos \alpha $.
2. Determine $sen\,\alpha $ e $\cos \alpha $, sabendo que $tg\,\alpha =-2$ e $-\frac{\pi }{2}<\alpha <0$.

Resolução >> Resolução

• Enunciado
• Resolução

Sabe-se que $\cos \alpha =\frac{1}{3}$.

1. Determine o valor exato de $sen\,\alpha $ e de $tg\,\alpha $, sabendo que $-\frac{\pi }{2}<\alpha <0$.
2. Determine o valor exato de $sen\,\alpha $ e de $tg\,\alpha $, sabendo que $\frac{3\pi }{2}<\alpha <2\pi $.

Resolução >> Resolução

• Enunciado
• Resolução

Na figura está representado um círculo trigonométrico de centro O e um pentágono regular [ABCDO].

1. Mostre que as coordenadas de B são $(1-\cos \alpha ;sen\,72{}^\text{o})$.
2. Determine uma expressão para obter a área do pentágono em função de $\alpha $ (em graus) e apresente um valor dessa área aproximada às décimas.

Resolução >> Resolução

• Enunciado
• Resolução

Uma professora de Matemática propôs aos seus alunos do 11.º X que encontrassem o melhor valor para a expressão \[sen\,(\frac{5}{6}\pi )-\cos \,(\frac{5}{4}\pi )+2sen\,(-\frac{25}{6}\pi )\]

O Rui, a Sara e a Inês apresentaram os seguintes resultados:

• Rui: $0,21$
• Sara: $\frac{3+\sqrt{2}}{2}$
• Inês: $\frac{\sqrt{2}-1}{2}$

Faça a sua própria pesquisa e comente cada um dos resultados apresentados por aqueles três alunos.

Resolução >> Resolução

• Enunciado
• Resolução

1. Desenhe um ângulo do 2.º quadrante cujo cosseno seja $-\frac{3}{4}$.
   Determine o valor exato do seno e da tangente.
2. Desenhe um ângulo do 4.º quadrante cuja tangente seja $-\frac{3}{2}$.
   Qual o valor exato do seno e do cosseno?

Resolução >> Resolução