A Casinha da Matemática Blog
Isometrias: Matematicamente Falando 8 - Pág. 96 Tarefa 9
Enunciado
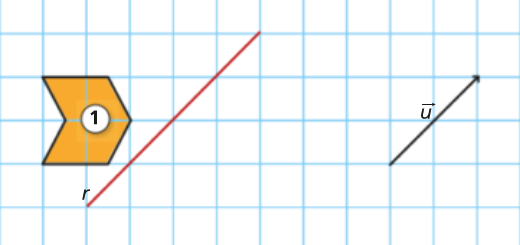
Copia a figura 1, a reta e o vetor \({\vec u}\).
- Obtém a figura 2, que é a imagem da figura 1 pela reflexão de eixo \(r\).
- Desenha a figura 3, que é o transformado da figura 2 pela translação de vetor \({\vec u}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 95 Ex. 2
Enunciado
A figura abaixo representa motivos de decoração de um tapete.
Sabendo que \(\vec u = \overrightarrow {AB} \) e \(\vec v = \overrightarrow {BC} \), determina a imagem de:
- \(A\) por \({T_{\vec v}}\)
- \(B\) por \({T_{ – \vec u}}\)
- \(D\) pela translação compostas das translações \({T_{\vec u}}\) e \({T_{ – \vec v}}\)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 95 Ex. 1
Enunciado
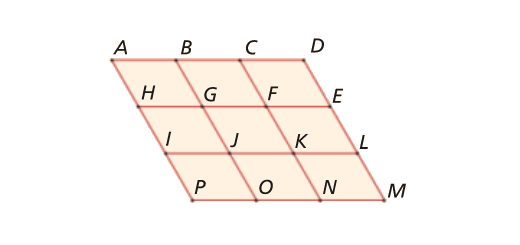
Na figura estão representados nove paralelogramos iguais.
Copia e completa, usando as letras da figura, cada uma das seguintes igualdades.
- \(F + \overrightarrow {DL} = \ldots \)
- \( \ldots + \overrightarrow {ML} = H\)
- \(O + \ldots = N\)
- \(\overrightarrow {JK} + \overrightarrow {EC} = \ldots \)
- \(\overrightarrow {PJ} + \overrightarrow {FE} + \overrightarrow {CF} = \ldots + \overrightarrow {CF} = \ldots \)
- \(\overrightarrow {HG} + \overrightarrow {OK} + \overrightarrow {DL} = \overrightarrow {HG} + \ldots =
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 94 Tarefa 8
Enunciado
Considera os vetores \({\vec u}\), \({\vec v}\) e \({\vec w}\).
- Copia os vetores para o teu caderno.
- Desenha e compara os vetores \(\vec a = \vec u + \vec v\) e \(\vec b = \vec v + \vec u\).
- Determina o vetor \(\vec c = \vec v + \vec w\).
- Desenha e compara os vetores \(\vec d = \vec a + \vec w\) e \(\vec f = \vec u + \vec c\).
- Desenha o vetor \(\vec g
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 4
Enunciado
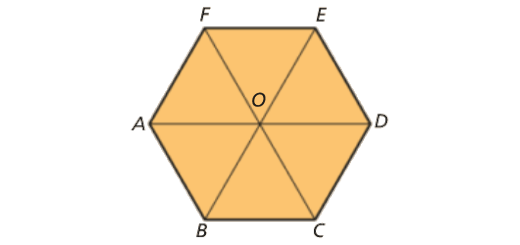
A figura representa um hexágono regular dividido em seis triângulos geometricamente iguais.
Usando letras da figura, determina:
- \(\overrightarrow {BC} + \overrightarrow {BO} \)
- \(\overrightarrow {OD} + \overrightarrow {BC} \)
- \(\overrightarrow {AB} + \overrightarrow {CF} \)
- \(\overrightarrow {DE} + \overrightarrow {FO} \)
- \(B + \overrightarrow {OE} \)
- \({T_{\overrightarrow {EF} }}\left( O \right)\)
- \(\left( {{T_{\overrightarrow {AF} }} \circ {T_{\overrightarrow {FO} }}} \right)\left( A \right)\)
- \(E + \overrightarrow {AB} \)
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 3
Enunciado
Determina \(\vec a + \vec b\) em cada caso.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 2
Enunciado
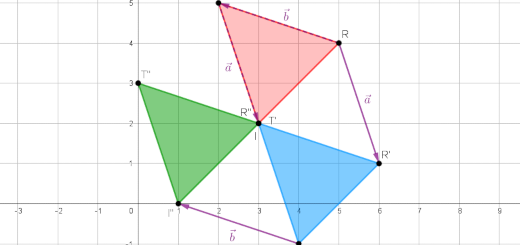
Considera o triângulo [TRI] cujas coordenadas são \(T\left( {2,5} \right)\), \(R\left( {5,4} \right)\), \(I\left( {3,2} \right)\) e os vetores \(\vec a = \overrightarrow {TI} \) e \(\vec b = \overrightarrow {RT} \).
- Desenha o triângulo [TRI] num sistema de eixos cartesianos.
- Aplica ao triângulo [TRI] a translação de vetor \(\vec a = \overrightarrow {TI} \).
Designa o novo triângulo por [T’R’I’].
- Aplica ao triângulo [T’R’I’ a translação de vetor \(\vec b = \overrightarrow {RT} \).
Designa o
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 93 Ex. 1
Enunciado
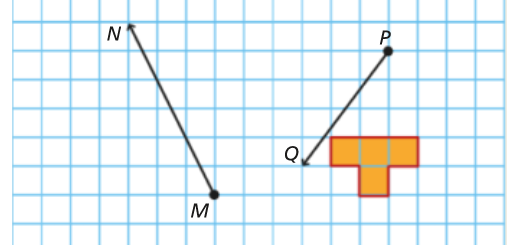
Copia a figura para o teu caderno.
Constrói a imagem do octógono pela translação de vetor \(\overrightarrow {MN} \), seguida da translação de vetor \(\overrightarrow {PQ} \).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 89 Tarefa 7
Enunciado
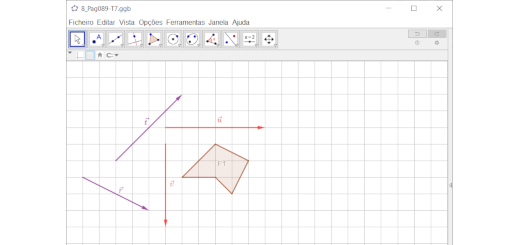
Observa a figura.
- Usando as quadrículas do teu caderno ou um programa de geometria dinâmica, como, por exemplo, o GeoGebra, reproduz a figura F1.
- Desenha a figura F2, imagem da figura F1, pela translação de vetor \({\vec u}\).
- Representa a figura F3, imagem da figura F2, pela translação de vetor \({\vec v}\).
- Há uma translação que transforma diretamente a figura F1 na figura F3.
Representa o vetor \({\vec w}\) dessa translação.
- Determina a figura F4, imagem
…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 88 Ex. 5
Enunciado
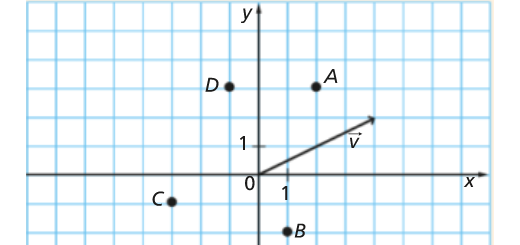
Observa os pontos marcados no referencial da figura.
- Indica as coordenadas dos pontos A, B e C.
- Marca o ponto N tal que \(\overrightarrow {DC} = \overrightarrow {AN} \).
Quais são as suas coordenadas?
- D é a imagem do ponto M pela translação de vetor \({\vec v}\). Quais são as coordenadas de M?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 88 Ex. 4
Enunciado
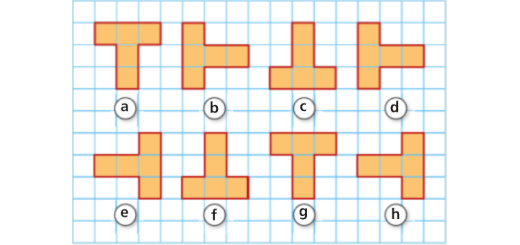
Observa as figuras seguintes.
- Indica as que se correspondem por uma translação.
- Indica o vetor associado a cada uma das translações encontradas na alínea anterior.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 88 Ex. 3
Enunciado
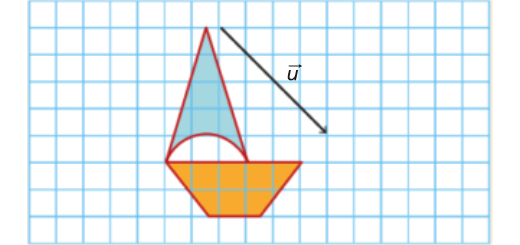
Constrói, no teu caderno, a imagem do barco pela translação de vetor \({\vec u}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 88 Ex. 2
Enunciado
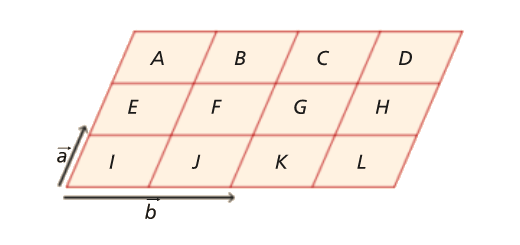
Na figura, estão representados doze paralelogramos iguais entre si.
- Qual é a imagem do paralelogramo G pela translação de vetor \({\vec a}\)?
- Qual é o transformado do paralelogramo B por \({T_{\vec b}}\)?
- Indica a translação que transforma F em J.
- Indica a imagem do paralelogramo H por \({T_{\vec 0}}\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Isometrias: Matematicamente Falando 8 - Pág. 88 Ex. 1
Enunciado
Considera o retângulo [ABCD].
Copia e completa as igualdades, usando as letras da figura.
- \(A + \overrightarrow {AB} = \ldots \)
- \(B + \overrightarrow {CD} = \ldots \)
- \(A + \ldots = D\)
- \( \ldots + \overrightarrow {BA} = D\)
Resolução >>
Resolução
<< Enunciado…
Ler mais















![Aproxima \(\sqrt[3]{5}\) às décimas](https://www.acasinhadamatematica.pt/wp-content/uploads/2017/10/9V1Pag024-8_520x245.png)




