Duas retas e uma circunferência
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 71 Ex. 12
Enunciado
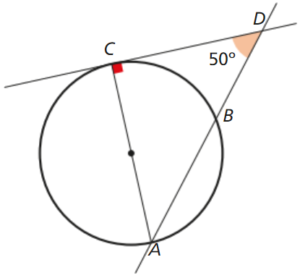Na figura, estão representadas as retas AD e CD e a circunferência de diâmetro [AC].
O ponto B pertence à circunferência e à reta AD.
Sabe-se que:
- a reta CD é tangente à circunferência no ponto C;
- \(C\widehat DA = 50^\circ \);
- \(\overline {CD} = 8\) cm.
A figura não está desenhada à escala.
- Qual é a amplitude, em graus, do arco CB?
[A] \(60^\circ \)
[B] \(70^\circ \)
[C] \(80^\circ \)
[D] \(90^\circ \) - Determina \(\overline {CA} \).
Apresenta o resultado em centímetros, arredondado às décimas.
Apresenta todos os cálculos que efetuares.
Resolução
Sabe-se que:
-
a reta CD é tangente à circunferência no ponto C;
-
\(C\widehat DA = 50^\circ \);
-
\(\overline {CD} = 8\) cm.
- No triângulo retângulo [ACD], os ângulos CAD e ADC são complementares. Logo, \(C\widehat AD = 90^\circ – A\widehat DC = 90^\circ – 50^\circ = 40^\circ \).
Assim, tendo em consideração que CAD é um ângulo inscrito, temos: \(BC = 2 \times C\widehat AD = 2 \times 40^\circ = 80^\circ \).
Portanto, a alternativa correta é a [C].
- No triângulo retângulo [ACD], temos:
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} A\widehat DC = \frac{{\overline {CA} }}{{\overline {CD} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} 50^\circ = \frac{{\overline {CA} }}{8}}\\{}& \Leftrightarrow &{\overline {CA} = 8 \times {\mathop{\rm tg}\nolimits} 50^\circ }\\{}&{}&{\overline {CA} \approx 9,5}\end{array}\]
Portanto, \(\overline {CA} \approx 9,5\) cm.
