Eixo de simetria do triângulo
Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 95 Ex. 7
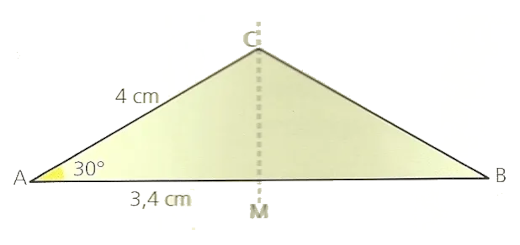
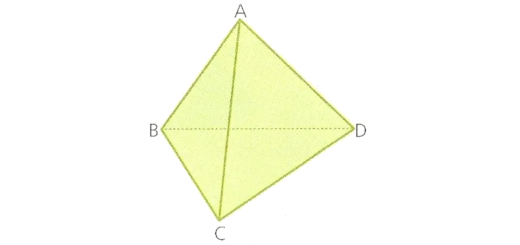
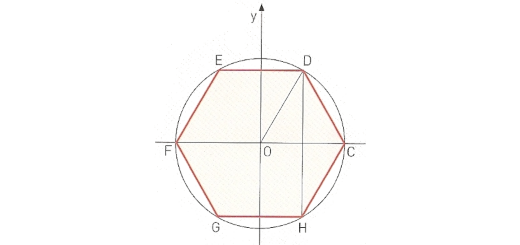
Observando a figura e sabendo que CM é eixo de simetria do triângulo [ABC], determina as amplitudes dos ângulos e as medidas dos comprimentos dos lados do triângulo.
Resolução >> Resolução
<< Enunciado