O pai do João comprou um terreno
Equações do 2.º grau: Matematicamente Falando 9 - Parte 2 Pág. 95 Ex. 8
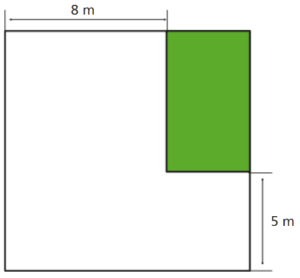O pai do João comprou um terreno com a forma de um quadrado.
Numa parte retangular desse terreno, o João vai fazer um jardim com 28 m2 de área, como mostra a figura.
Qual é a medida do lado do terreno?
Explica a tua resposta.
Seja x, em metros, o comprimento do lado do terreno com a forma quadrada.
A área do jardim pode ser expressa, em função de x, por:
\[\begin{array}{*{20}{l}}{{A_{Jardim }}}& = &{\left( {x – 8} \right)\left( {x – 5} \right)}\\{}& = &{{x^2} – 5x – 8x + 40}\\{}& = &{{x^2} – 13x + 40}\end{array}\]
com \(x > 8\).
Como o jardim terá 28 m2 de área, vem:
\[\begin{array}{*{20}{l}}{{A_{Jardim }} = 28}& \Leftrightarrow &{\begin{array}{*{20}{c}}{{x^2} – 13x + 40 = 28}& \wedge &{x > 8}\end{array}}\\{}& \Leftrightarrow &{\begin{array}{*{20}{c}}{{x^2} – 13x + 12 = 0}& \wedge &{x > 8}\end{array}}\\{}& \Leftrightarrow &{\begin{array}{*{20}{c}}{x = \frac{{13 \mp \sqrt {169 – 48} }}{2}}& \wedge &{x > 2}\end{array}}\\{}& \Leftrightarrow &{\begin{array}{*{20}{c}}{\left( {\begin{array}{*{20}{c}}{x = \frac{{13 – 11}}{2}}& \vee &{x = \frac{{13 + 11}}{2}}\end{array}} \right)}& \wedge &{x > 2}\end{array}}\\{}& \Leftrightarrow &{x = 12}\end{array}\]
Portanto, o terreno tem 8 m de lado.
