A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Category: Aplicando

0

Aplicando / 11.º Ano / Funções racionais

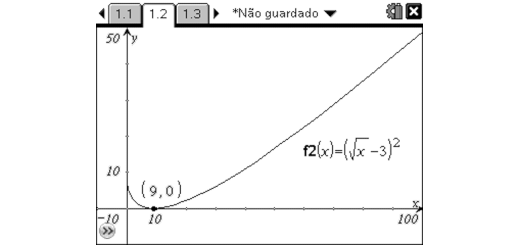
A intensidade do som

Função potência: Infinito 11 A - Parte 2 Pág. 209 Ex. 98

Enunciado

A intensidade do som pode ser medida em Watt por metro quadrado, medida da pressão que o som exerce sobre o nosso ouvido. A intensidade do som emitido por uma aparelhagem sonora é função da distância a que o ouvinte se encontra das colunas de som. Na tabela seguinte estão registados os resultados de algumas medições efetuadas a diferentes distâncias das colunas de uma certa aparelhagem de som:

  1. Descreva o modelo global que relaciona a distância
… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Considere as funções

Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 94

Enunciado

Considere as funções definidas em $\mathbb{R}$ por:

$f(x)=\frac{3x}{{{x}^{2}}-4}$ $f(x)=\frac{{{x}^{2}}}{x+2}$ $f(x)=\sqrt{{{x}^{2}}-4}$
$f(x)=\left| {{x}^{2}}-4 \right|$ $f(x)=\frac{{{x}^{2}}-4}{{{x}^{2}}}$

$f(x)=\frac{{{x}^{3}}}{{{x}^{2}}-9}$
  • Determine o domínio das funções dadas.
  • Calcule, para cada uma delas: $f(-x)$, $f(x-2)$ e $-f(x)$.
  • Algumas das funções é par? E ímpar?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

A função polinomial definida por $f(x)={{x}^{4}}$ não é injetiva

Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 93

Enunciado

A função polinomial definida por $f(x)={{x}^{4}}$ não é injetiva.

Encontre uma restrição g da função f de modo que g seja injetiva.

Caracterize ${{g}^{-1}}$.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Sendo f e g funções reais de variável real

Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 85

Enunciado

Sendo f e g funções reais de variável real, caracterize $f\circ g$ e $g\circ f$, em cada um dos casos:

  1. $\begin{matrix}
    f(x)=\sqrt{x} & \text{e} & g(x)={{x}^{2}}+1  \\
    \end{matrix}$
  2. $\begin{matrix}
    f(x)={{(x-1)}^{3}} & \text{e} & g(x)=\sqrt[3]{x}+1  \\
    \end{matrix}$

Resolução >> Resolução

<< Enunciado… Ler mais
0

11.º Ano / Funções com radicais / Aplicando

Um quadro de sinal

Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 83

Enunciado

O quadro seguinte dá-nos o sinal de uma função f, definida em $\mathbb{R}$:

Determine o domínio das funções seguintes:

  1. ${{f}_{1}}:x\to \frac{1}{f(x)}$
  2. ${{f}_{2}}:x\to \sqrt{f(x)}$
  3. ${{f}_{3}}:x\to \frac{1}{\sqrt{f(x)}}$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Determine, em R, o domínio das funções

Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 82

Enunciado

Determine, em $\mathbb{R}$, o domínio das funções:

  1. $f:x\to \sqrt{-x}$
  2. $g:x\to \sqrt{\frac{x-3}{x-4}}$
  3. $h:x\to \sqrt{-{{x}^{2}}+4x}$
  4. $i:x\to \frac{\sqrt{x-3}}{\sqrt{x-4}}$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Considere as funções reais de variável real

Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 81

Enunciado

Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to {{(\sqrt{x}+3)}^{2}} & \text{e} & g:x\to {{(\sqrt{x}-3)}^{2}}  \\
\end{matrix}\]

  1. Determine o domínio de f e de g.
  2. Determine, se existirem, os zeros de f e de g.
  3. Caracterize as funções $(f+g)$ e  $(f\times g)$ e apresente as expressões de $(f+g)(x)$ e $(f\times g)(x)$ na forma mais simplificada possível.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Verifique se são iguais as funções

Funções com radicais: Infinito 11 A - Parte 2 Pág. 205 Ex. 80

Enunciado

Verifique se são iguais as funções reais de variável real, f e g, assim definidas:

  1. $\begin{matrix}
    f:x\to \sqrt{{{(-x)}^{2}}} & {} & g:x\to \left| x \right|  \\
    \end{matrix}$
  2. $\begin{matrix}
    f:x\to \sqrt{x}.\sqrt{x} & {} & g:x\to x  \\
    \end{matrix}$
  3. $\begin{matrix}
    f:x\to \sqrt{x+1}.\sqrt{x-1} & {} & g:x\to \sqrt{{{x}^{2}}-1}  \\
    \end{matrix}$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Funções com radicais

Considere as funções reais de variável real

Funções com radicais: Infinito 11 A - Parte 2 Pág. 205 Ex. 79

Enunciado

Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to \sqrt{x-2}+1 & {} & g:x\to \sqrt{2{{x}^{2}}-9}-x  \\
\end{matrix}\]

  1. Determine os domínios de f e de g.
  2. Determine os zeros de cada uma das funções.

Resolução >> Resolução

<< Enunciado… Ler mais
0

11.º Ano / Função inversa / Aplicando

Use a calculadora gráfica

Função inversa: Infinito 11 A - Parte 2 Pág. 204 Ex. 75

Enunciado

  1. Use a calculadora gráfica e conjeture quais das seguintes funções polinomiais têm função inversa:
    ${{f}_{1}}(x)={{x}^{3}}-9{{x}^{2}}+5x-5$ ${{f}_{2}}(x)=2x+{{x}^{2}}$ ${{f}_{3}}(x)={{x}^{3}}-2{{x}^{2}}+5x-5$
    ${{f}_{4}}(x)=2x-{{x}^{2}}$ ${{f}_{5}}(x)=2x+{{x}^{3}}$ ${{f}_{6}}(x)=2x-{{x}^{3}}$
  2. Para as que admitiu serem funções injetivas, calcule a imagem, pela inversa, de 10, com aproximação às centésimas.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Função inversa

Qual o valor lógico das proposições?

Função inversa: Infinito 11 A - Parte 2 Pág. 204 Ex. 74

Enunciado

Qual o valor lógico das proposições?

  1. A função $f:x\to {{x}^{2}}-2$ admite função inversa.
  2. Nenhuma função par admite função inversa.
  3. Algumas funções ímpares admitem função inversa.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Função composta / Aplicando / 11.º Ano

Dadas as funções

Função composta: Infinito 11 A - Parte 2 Pág. 203 Ex. 71

Enunciado

Dadas as funções definidas em $\mathbb{R}$ por \[\begin{matrix}
f(x)=3x-4 & e & g(x)=\frac{1}{x}  \\
\end{matrix}\]

  1. Determine:
    $(f+g)(5)$ $(f-g)(5)$ $(f\times g)(5)$ $(f\div g)(5)$
    $(f\circ g)(5)$ $(g\circ f)(5)$ $(f\circ f)(5)$ $(g\circ g)(5)$
  2. Caracterize as funções:
    $f+g$ $f-g$ $f\times g$ $f\div g$
    $f\circ g$ $g\circ f$ $f\circ f$ $g\circ g$

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 11.º Ano / Função composta

Sendo $f$ e $g$ funções reais de variável real

Função composta: Infinito 11 A - Parte 2 Pág. 202 Ex. 66

Enunciado

Sendo $f$ e $g$ funções reais de variável real, caracterize $f\circ g$ e $g\circ f$ em cada um dos casos:

  1. $\begin{matrix}
    f(x)={{x}^{2}}+2x+1 & e & g(x)=3{{x}^{2}}+1  \\
    \end{matrix}$
  2. $\begin{matrix}
    f(x)={{x}^{2}}+2x & e & g(x)=\left| x \right|+1  \\
    \end{matrix}$
  3. $\begin{matrix}
    f(x)={{x}^{3}} & e & g(x)=\frac{1}{x-3}  \\
    \end{matrix}$

Resolução >> Resolução

<< Enunciado… Ler mais