Category: Decomposição de figuras – Teorema de Pitágoras

• Enunciado
• Resolução

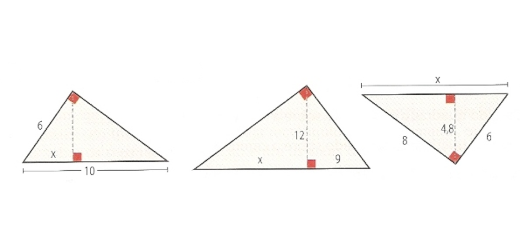
No triângulo equilátero ao lado, determina um valor aproximado às décimas:

1. da medida da altura;
2. da área.

Resolução >> Resolução

• Enunciado
• Resolução

Qual é a medida da diagonal de um quadrado cujo perímetro mede 24 cm? Justifica.

Resolução >> Resolução

• Enunciado
• Resolução

Cada arco é uma semicircunferência.

1. Calcula a área de cada um dos semicírculos, supondo que os catetos do triângulo retângulo têm 8 cm e 6 cm de comprimento.
2. Relaciona as áreas dos três semicírculos.

Resolução >> Resolução

• Enunciado
• Resolução

Observa a figura em que os vértices dos ângulos retos formam uma espiral.

Calcula a, b, c, d e e.

Resolução >> Resolução

• Enunciado
• Resolução

Ao lado, desenhámos a vista frontal de uma casa.

Calcula:

1. a altura h do telhado;
2. o comprimento c.

Resolução >> Resolução

• Enunciado
• Resolução

O seguinte problema é adaptado do livro chinês Nove Capítulos da Arte Matemática, so séc. I a.C.

Um bambu partiu-se, a uma altura do chão de 2,275 m, e a parte de cima, ao cair, tocou o chão, a uma distância de 1,5 m da base do bambu.

Qual era a altura do bambu, antes de se ter partido?

Resolve o problema e apresenta todos os cálculos que efetuares.

Resolução >> Resolução