Três semicírculos
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 32 Ex. 7
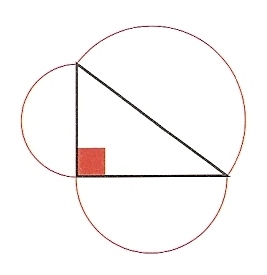Cada arco é uma semicircunferência.
- Calcula a área de cada um dos semicírculos, supondo que os catetos do triângulo retângulo têm 8 cm e 6 cm de comprimento.
- Relaciona as áreas dos três semicírculos.
Comecemos por determinar o comprimento da hipotenusa:
$$\begin{array}{*{35}{l}}
{{h}^{2}}={{6}^{2}}+{{8}^{2}} & \Leftrightarrow & {{h}^{2}}=36+64 \\
{} & \Leftrightarrow & {{h}^{2}}=100 \\
{} & Logo, & h=10 \\
\end{array}$$Tendo em conta que a fórmula para calcular a área de um círculo é ${{A}_{C\acute{i}rculo}}=\pi {{r}^{2}}$, temos:
Área do semicírculo pequeno: \[{{A}_{SCp}}=\frac{\pi \times {{3}^{2}}}{2}=\frac{9\pi }{2}\,\,c{{m}^{2}}\]
Área do semicírculo médio: \[{{A}_{SCm}}=\frac{\pi \times {{4}^{2}}}{2}=\frac{16\pi }{2}\,\,c{{m}^{2}}\]
Área do semicírculo grande: \[{{A}_{SCg}}=\frac{\pi \times {{5}^{2}}}{2}=\frac{25\pi }{2}\,\,c{{m}^{2}}\]
-
Comparando as áreas determinadas, conclui-se: \[{{A}_{SCp}}+{{A}_{SCm}}=\frac{9\pi }{2}+\frac{16\pi }{2}=\frac{25\pi }{2}={{A}_{SCg}}\]
A soma das áreas dos semicírculos sobre os catetos é igual à área do semicírculo sobre a hipotenusa.
EXCELENTE