A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

A Casinha da Matemática Blog

1

Decomposição de figuras - Teorema de Pitágoras / Aplicando / 8.º Ano

Calcula o valor de x em cada triângulo

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 25 Ex. 15

Enunciado

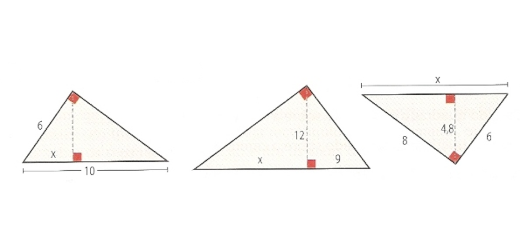
Calcula o valor de x em cada um dos seguintes triângulos (a unidade de comprimento é o centímetro):

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Dois insetos

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 25 Ex. 14

Enunciado

Um inseto parte do ponto M e percorre os segmentos [MA] e [AC], parando no ponto C.

Um outro inseto parte do ponto C e percorre os segmentos [CB] e [BM], parando no ponto M.

  1. Prova que os triângulos [AMC] e [CMB] são semelhantes.
  2. Determina:
    – a distância que separa os dois insetos;
    – a distância percorrida pelo primeiro inseto.

 Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Desenha um rectângulo [ABCD]

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 25 Ex. 11

Enunciado

Desenha um retângulo [ABCD] com $\overline{AD}=9\,cm$ e $\overline{BC}=5\,cm$.

Traça a diagonal [AC] e determina o baricentro do triângulo [ABC] e o baricentro do triângulo [ACD].

A que segmento pertencem os dois baricentros?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Decomposição de figuras - Teorema de Pitágoras / Aplicando / 8.º Ano

A área da casa

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 24 Ex. 9

Enunciado

A Maria está a pensar comprar casa.

Numa imobiliária mostraram-lhe a planta ao lado.

Ajuda-a a determinar a área a casa.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Decomposição de figuras - Teorema de Pitágoras / Aplicando / 8.º Ano

Calcula a área das figuras

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 24 Ex. 8

Enunciado

Calcula a área das figuras decompondo-as em triângulos e/ou quadriláteros, considerando as medidas indicadas expressas em centímetros.

Resolução >> Resolução

<< Enunciado… Ler mais
1

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Um telhado de quatro águas

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 24 Ex. 7

Enunciado

Há casas construídas com telhados de duas águas e outras com telhados de quatro águas.

Na figura está representado um telhado com quatro águas. Os números indicam as medidas em metros.


 Sabendo que para cobrir 1 m2 desse telhado são necessárias 15 telhas:

  1. quantas telhas, no mínimo, serão utilizadas para cobrir esse telhado, se na cobertura houver uma perda de 3%?
  2. se dez telhas custam 5 €, quanto custará esse telhado?

Resolução >> Resolução

<< Enunciado… Ler mais
2

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Calcula a área do trapézio

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 24 Ex. 6

Enunciado

Calcula a área do trapézio:

  1. decompondo-o em dois triângulos e um quadrado;
  2. usando a fórmula para determinar a área de um trapézio.

Resolução >> Resolução

<< Enunciado… Ler mais
0

8.º Ano / Decomposição de figuras - Teorema de Pitágoras / Aplicando

Determina as áreas

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 23 Ex. 5

Enunciado

Considerando a figura ao lado, determina a área:

  1. do retângulo [ABCD];
  2. do triângulo [BMC];
  3. do trapézio [ABME].

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Os triângulos do Pedro

Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 23 Ex. 3

Enunciado

O Pedro desenhou duas retas paralelas.

Numa marcou os pontos C, D, E e F, na outra os pontos A e B, como mostra a figura.

Em seguida, uniu alguns pontos formando os triângulos [CAB], [DAB], [EAB] e [FAB].

Analisando esses triângulos, o Pedro descobriu um “segredo” sobre as suas áreas.

Qual foi o segredo descoberto pedo Pedro?
Resolução >> Resolução

<< Enunciado… Ler mais
0

Decomposição de figuras - Teorema de Pitágoras / Aplicando / 8.º Ano

Área do trapézio

Qual será a fórmula da área do trapézio?

  1. Sem ativar a opção “Mostrar Fórmula” e manipulando a figura, tenta descobrir como calcular a área do trapézio.
  2. A área do trapézio é igual à área de um triângulo.
    Qual? Porquê?
  3. Ativa a opção “Mostrar Fórmula” e prova a fórmula apresentada.
0

Aplicando / 8.º Ano / Decomposição de figuras - Teorema de Pitágoras

Área do paralelogramo

Qual será a fórmula da área do paralelogramo?

  1. Sem ativar as opções e manipulando a figura, tenta descobrir como calcular a área do paralelogramo.
  2. Ativa a opção “Mostrar decomposição”. Já estás mais seguro da tua suposição?
  3. Ativa a opção “Mostrar Fórmula” e verifica se a tua suposição estava correta.
  4. Prova, agora, a fórmula apresentada.
0

Geometria Analítica / Aplicando / 11.º Ano

Determine uma equação cartesiana do plano mediador do segmento [AB]

Geometria Analítica: Infinito 11 A - Parte 1 Pág. 181 Ex. 31

Enunciado

Determine uma equação cartesiana do plano mediador do segmento de reta [AB], sendo:

  1. $A(4,-1,2)$ e $B(2,7,0)$.
  2. $A(-4,1,7)$ e $B(3,2,-5)$.

Resolução >> Resolução

<< Enunciado… Ler mais