Numa escola secundária
Probabilidades e combinatória: Infinito 12 A - Parte 1 Pág. 171 Ex. 29
Numa Escola Secundária fez-se um estudo sobe o número de alunos do 12.º ano que se matricularam nas disciplinas de Física e de Química, tendo-se concluído que:
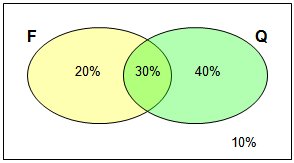
- 30% dos alunos matricularam-se em ambas;
- 20% dos alunos matricularam-se apenas em Física;
- 40% dos alunos matricularam-se apenas em Química.
- Construa um diagrama de Venn para ilustrar a situação.
- Considere os acontecimentos F: “Matricular-se em Física” e Q: “Matricular-se em Química”.
Determine a probabilidade de um desses alunos submetido ao estudo:a) matricular-se em Física ou em Química;
b) matricular-se em Física, dado que se matriculou em Química;
c) não se matricular em Física, dado que se matriculou em Química;
d) matricular-se em Química, dado que não se matriculou em Física.
- É mais provável um aluno matricular-se em Física se se matriculou em Química ou se não se matriculou em Química?
- Justifique que os acontecimentos F e Q não são independentes.
Apresenta-se ao lado um diagrama de Venn para ilustrar a situação.
- Sejam F: “Matricular-se em Física” e Q: “Matricular-se em Química”.
a) matricular-se em Física ou em Química;
Ora, $P(F\cup Q)=P(F)+P(Q)-P(F\cap Q)=0,5+0,7-0,3=0,9$.
A probabilidade pedida é 90%.b) matricular-se em Física, dado que se matriculou em Química;
A probabilidade pedida é: \[P(F|Q)=\frac{P(F\cap Q)}{P(Q)}=\frac{0,3}{0,7}=\frac{3}{7}\]
c) não se matricular em Física, dado que se matriculou em Química;
A probabilidade pedida é: \[P(\overline{F}|Q)=\frac{P(\overline{F}\cap Q)}{P(Q)}=\frac{0,4}{0,7}=\frac{4}{7}\]
d) matricular-se em Química, dado que não se matriculou em Física.
A probabilidade pedida é: \[P(Q|\overline{F})=\frac{P(\overline{F}\cap Q)}{P(\overline{F})}=\frac{0,4}{1-0,5}=\frac{4}{5}\]
- É mais provável um aluno matricular-se em Física se se matriculou em Química ou se não se matriculou em Química?
Já vimos que $P(F|Q)=\frac{3}{7}$.
Por outro lado: \[P(F|\overline{Q})=\frac{P(F\cap \overline{Q})}{P(\overline{Q})}=\frac{0,2}{1-0,7}=\frac{2}{3}\]
Logo, é mais provável um aluno matricular-se em Física se se não matriculou em Química, pois $P(F|\overline{Q})>P(F|Q)$.
- Justifique que os acontecimentos F e Q não são independentes.
Como $P(F\cap Q)=0,3$ e $P(F)\times P(Q)=0,5\times 0,7=0,35$, então $P(F\cap Q)\ne P(F)\times P(Q)$ e, por isso, os acontecimentos F e Q não são independentes.
Trabalho realizado por João Melo, que frequenta(ou) a Escola Secundária/2,3 da Sé, em Lamego.
