O quintal do João
Números inteiros: Matematicamente Falando 7 - Pág. 39 Ex. 7
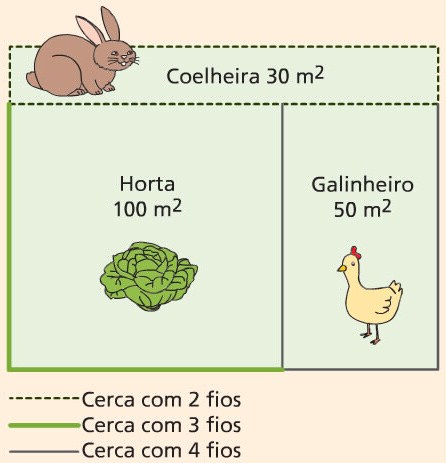 O João tem um terreno retangular onde há um galinheiro e uma coelheira também retangulares e uma horta quadrada, cujas medidas de área estão indicadas na figura.
O João tem um terreno retangular onde há um galinheiro e uma coelheira também retangulares e uma horta quadrada, cujas medidas de área estão indicadas na figura.
O João cercou a horta, o galinheiro e a coelheira com cercas feitas com diferentes números de fios de arame, como indicado na figura.
Quantos metros de arame ele usou?
 O comprimento do lado da horta é ${l_H} = \sqrt {100} = 10$ m.
O comprimento do lado da horta é ${l_H} = \sqrt {100} = 10$ m.
O galinheiro e a horta têm iguais comprimentos. Logo, o comprimento do galinheiro é ${c_G} = 10$ m.
Como a área de um retângulo pode ser expressa por ${A_{\operatorname{Re} tângulo}} = c \times l$, então a largura do galinheiro é ${l_G} = \frac{{50}}{{10}} = 5$ m.
Assim, a coelheira tem ${c_C} = {l_H} + {l_G} = 10 + 5 = 15$ m de comprimento.
E, por último, a coelheira tem ${l_C} = \frac{{30}}{{15}} = 2$ m de largura.
Quantidade de arame usado na cerca da coelheira: $2 \times \left( {2 \times 15 + 2 \times 2} \right) = 2 \times 34 = 68$ m.
Quantidade de arame gasto na cerca tripla da horta: $3 \times \left( {10 + 10} \right) = 60$ m.
Quantidade da arame gasto na cerca quádrupla do galinheiro: $4 \times \left( {2 \times 10 + 5} \right) = 100$ m.
Portanto, o João usou $68 + 60 + 100 = 228$ m de rede nas suas cercas.



















O problema está resolvido nesta página, na aba “Resolução”.
qual a resposta pfv!