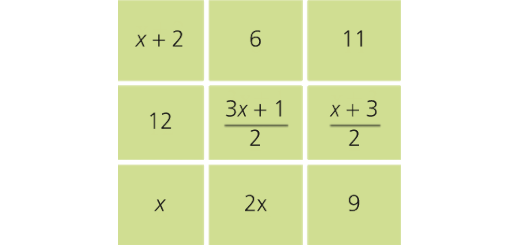A Casinha da Matemática Blog
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 190 Ex. 3
Enunciado
Resolve cada uma das seguintes equações:
- \[u + 3v = 5\] em ordem a u e em ordem a v;
- \[\frac{{3x + y}}{2} = 3\] em ordem a x e em ordem a y.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 190 Ex. 2
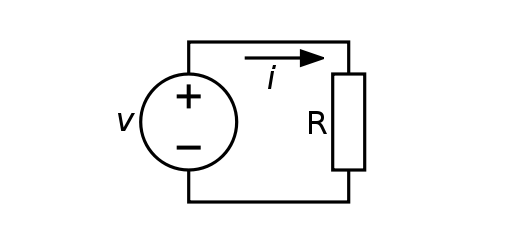
Enunciado
Num circuito elétrico, a diferença de potencial (V) entre dois pontos está relacionada com a intensidade da corrente que o percorre (I) e com a resistência do circuito (R) segundo a fórmula \(V = RI\).
- Qual é a diferença de potencial (em volt) num circuito quando a intensidade da corrente é 12 ampere e a sua resistência é 20 ohm?
- Resolve a equação dada:
a) em ordem a R;
b)
…
Ler mais
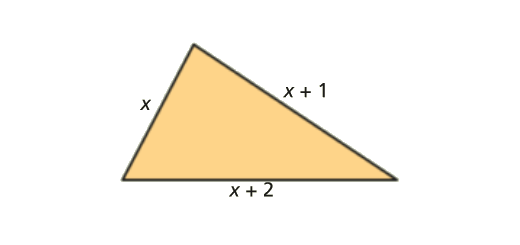
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 190 Ex. 1
Enunciado
Considera o triângulo da figura.
As medidas estão expressas em cm.
- Escreve uma expressão literal que te permita calcula o perímetro P do triângulo.
- Qual é o perímetro do triângulo se \(x = \frac{2}{3}\)?
- Obtiveste em 1. uma equação com duas variáveis, P e x, resolvida em ordem a P.
Resolve-a em ordem a x.
- Qual é o comprimento dos lados do triângulo se o perímetro for 9 cm?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 189 Tarefa 6
Enunciado
Um quadrado, de lado x, tem perímetro p e área a (p>0 e a>0).
- Escreve uma igualdade que relacione x e p e outra que relacione x e a.
- Resolve cada uma das equações em ordem a x e deduz que \({p^2} = 16a\).
- Existe algum quadrado de perímetro 20 cm e de área 24 cm2?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 189 Tarefa 5
Enunciado
A escala térmica usada, por exemplo, em Inglaterra é a escala Fahrenheit.
Quando a água gela, os termómetros ingleses marcam 32 °F.
Quando a água ferve, esses termómetros marcam 212 °F.
A relação entre graus Celsius (C) e os graus Fahrenheit (F) é a seguinte:
\[\frac{{F – 32}}{9} = \frac{C}{5}\]
- A quantos graus Celsius correspondem a 32 °F?
- E 32 °C a quantos graus Fahrenheit correspondem?
- Copia e completa a tabela, usando, quando necessário, valores aproximados
…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 187 Tarefa 4
Enunciado
O André e a Marta estavam a jogar ao jogo do Mikado.
A dada altura, o jogo da Marta apresentava-se da seguinte maneira.
Que posição relativa de retas te sugere:
- a vareta verde em relação à vermelha e à amarela?
- a vareta azul em relação à verde?
- a vareta branca em relação à vermelha?
Resolução >>
Resolução
O André e a Marta estavam a jogar ao jogo do Mikado.
A dada altura, o jogo da Marta apresentava-se
…
Ler mais
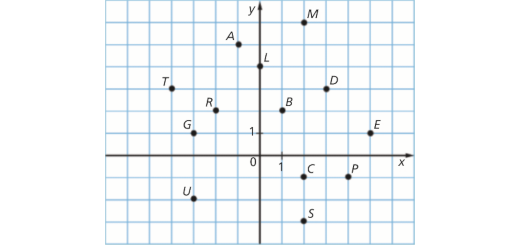
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 187 Tarefa 3
Enunciado
A palavra a descobrir é composta por sete letras da figura abaixo.
Para descobrir cada uma dessas letras, não necessariamente pela ordem em que se encontram na palavra, procura o ponto cuja:
- abcissa é superior a 4;
- abcissa é inferior a −3;
- abcissa é igual à ordenada;
- abcissa é simétrica da ordenada;
- ordenada é inferior a −2;
- ordenada está compreendida entre −1 e −3;
- abcissa está compreendida entre −0,5 e −1,5.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 186 Tarefa 2
Enunciado
Observa o seguinte quadrado mágico aditivo (a soma dos valores de cada linha, coluna ou diagonal é sempre a mesma).
Determina o valor de x.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações literais e sistemas: Matematicamente Falando 8 - Pág. 186 Tarefa 1
Enunciado
Na construção seguinte, cada número é a soma dos dois números que estão nas casas imediatamente abaixo.
- Escreve uma equação que te permita determinar o valor de x.
- Qual é o primeiro membro desta equação? E o 2.º?
- Que termos constituem o 1.º membro? E o 2.º?
- Determina o valor de x.
- Classifica a equação obtida em 1.
- Qual é o número que está no cimo da construção?
Resolução >>
Resolução
<< Enunciado…
Ler mais
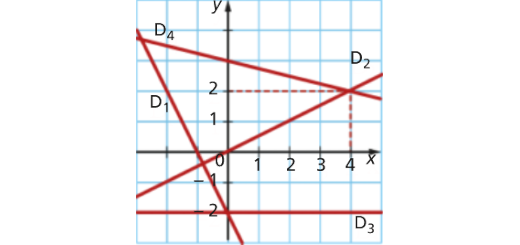
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 181 Ex. 5
Enunciado
As funções f, g, h e j têm como representações gráficas D1, D2, D3 e D4.
- A função f é uma função linear e \(f\left( 4 \right) = 2\);
- \(g\left( 0 \right) = 3\);
- a representação gráfica da função h é uma reta de declive \( – 2\);
- a função j é constante.
- Associa cada representação gráfica à função que lhe corresponde.
- Escreve uma expressão algébrica de cada
…
Ler mais
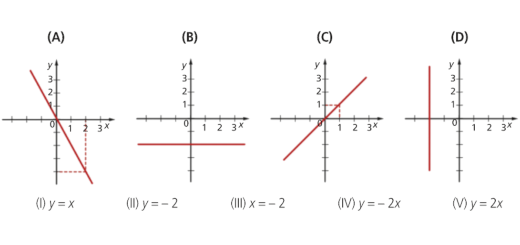
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 181 Ex. 4
Enunciado
Associa cada reta (A), (B), (C) e (D) à equação que lhe corresponde.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 181 Ex. 3
Enunciado
O pai da Ana foi contratado para vender um modelo de computadores, cujo preço unitário é de 600 euros. Por mês, ele recebe uma quantia fixa de 200 euros. Para além desse valor, recebe ainda, por cada computador que vender, 12% do seu preço.
- Qual é o número mínimo de computadores que ele terá de vender, num determinado mês, para receber mais do que 1500 euros, nesse mês?
- Designa por f a função que faz corresponder ao
…
Ler mais
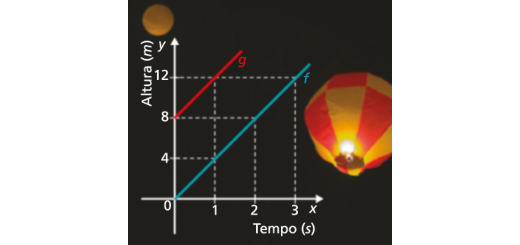
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 180 Ex. 2
Enunciado
Nos gráficos, mostra-se a correspondência entre o tempo decorrido desde o lançamento e a altura a que se encontram dois balões de S. João, tendo um deles sido lançado do chão e outro do cimo de um prédio.
- Uma das funções é de proporcionalidade direta.
Identifica-a, justificando, e determina a constante de proporcionalidade.
- Qual é a função que corresponde ao balão lançado do cimo do prédio? De que altura foi lançado? Justifica.
- Determina \(f\left( 2 \right)\) e
…
Ler mais
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 180 Ex. 1
Enunciado
A tabela seguinte relaciona o preço das motas de um determinado fabricante com a sua cilindrada.
- “O custo de cada mota é função da sua cilindrada”.
Justifica esta afirmação.
- Indica:
a) A variável dependente e a variável independente.
b) O domínio e o contradomínio da função.
c) A imagem de 350.
d) O objeto cuja imagem é 13500.
- Designando por f a função representada na tabela:
a) Explica o significado da expressão \(f\left( {500} \right) = 9000\)
…
Ler mais