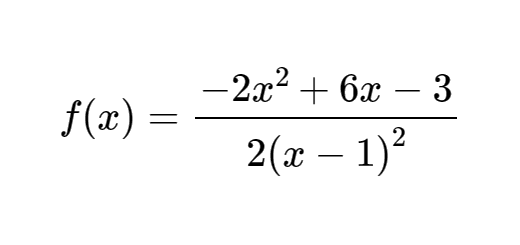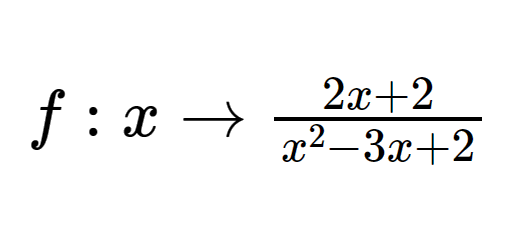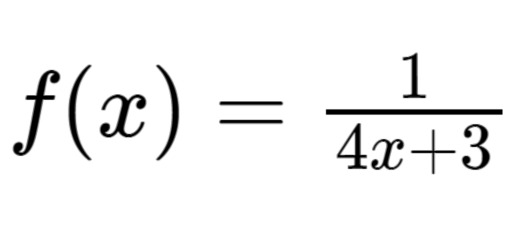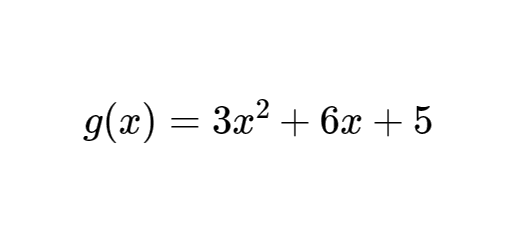A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)
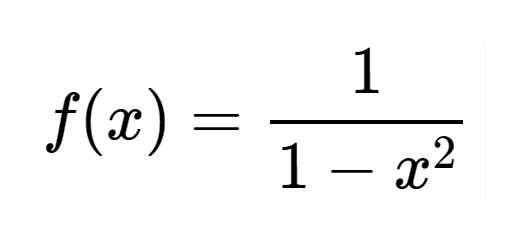
f é uma função racional definida em $\mathbb{R}\backslash \left\{ -1,1 \right\}$ por \[f(x)=\frac{1}{1-{{x}^{2}}}\]
Encontre os reais a e b tais que, para todo o $x\ne 1\wedge x\ne -1$, \[f(x)=\frac{a}{1-x}+\frac{b}{1+x}\]
Resolução >> Resolução
<< Enunciado… Ler maisf é uma função racional definida em $\mathbb{R}\backslash \left\{ 1 \right\}$ por \[f(x)=\frac{-2{{x}^{2}}+6x-3}{2{{(x-1)}^{2}}}\]
Encontre os reais a, b e c tais que, para todo o $x\ne 1$, \[f(x)=a+\frac{b}{x-1}+\frac{c}{2{{(x-1)}^{2}}}\]
Resolução >> Resolução
<< Enunciado… Ler maisSejam \[\begin{matrix}
f:x\to \frac{2x+2}{{{x}^{2}}-3x+2} & e & g:x\to \frac{4x-4}{x-2} \\
\end{matrix}\]
Resolução >> Resolução
<< Enunciado… Ler maisSejam: \[\begin{matrix}
f:x\to \frac{3x-4}{{{(x-1)}^{2}}} & e & g:x\to \frac{4}{{{x}^{3}}-1} \\
\end{matrix}\]
Mostre que $f+g$ é uma função racional e determine o seu domínio.
Resolução >> Resolução
<< Enunciado… Ler maisSejam as funções racionais definidas por: \[\begin{matrix}
f(x)=\frac{1}{4x+3} & e & g(x)=\frac{2x-1}{(4x+3)(x-7)} \\
\end{matrix}\]
Resolução >> Resolução
<< Enunciado… Ler maisUm objeto move-se ao longo de uma reta e a sua distância, em centímetros, a um ponto de referência fixo é dada em função do tempo t, em segundos, por \[\begin{matrix}
d\,(t)=2\,t+\frac{8}{t+1} & (t\ge 0) \\
\end{matrix}\]
Recorrendo exclusivamente a processos analíticos, resolva as três alíneas seguintes.
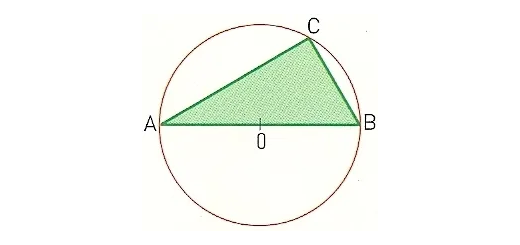
O triângulo [ABC] está inscrito num semicírculo de diâmetro 15 cm.
Resolução >> Resolução
<< Enunciado… Ler maisComo resultado de uma pesquisa de mercado, o diretor de uma empresa verificou que a procura dos seus produtos era dada, aproximadamente, por uma função linear de equação \[v=30-2p\] em que v representa a procura, ou seja, o número de artigos (em milhões) que serão vendidos ao preço de p euros.
Se forem vendidos v artigos ao preço de p euros, então o rendimento r da empresa (em milhões de euros) será dado por: \[r=vp=(30-2p)p=30p-2{{p}^{2}}\]
A densidade populacional (número de habitantes por unidade de área) de muitas cidades depende, grosseiramente, da distância ao centro da cidade.
Para uma determinada cidade, a densidade populacional P, em milhares de pessoas por km2, à distância de r quilómetros do centro, é dada, aproximadamente, por: \[P=5+30r-15{{r}^{2}}\]
Uma folha retangular de metal com 20 cm de largura vai ser dobrada para se fabricarem caleiras, como mostra a figura.
Por onde devem ser feitas as dobragens para que a caleira transporte a maior quantidade possível de água?
Resolução >> Resolução
<< Resolução… Ler maisConsidere a função quadrática definida por $g(x)=3{{x}^{2}}+6x+5$.
Resolução >> Resolução
<< Enunciado… Ler maisLançou-se um foguete de fabrico artesanal. Devido a um defeito de fabrico, o foguete começa a perder altura, mas, em seguida, recupera e sobe de novo. A altura a (em metros) a que se encontra é dada, em função do tempo t decorrido (em segundos) após o seu lançamento, por: \[\begin{matrix}
a(t)={{t}^{3}}-9{{t}^{2}}+24t & (0\le t\le 7) \\
\end{matrix}\]
Considerando o retângulo de visualização [-100, 100] por [-500, 500], pronuncie-se sobre o comportamento das duas funções para valores muito grandes de $\left| x \right|$.
Os navios possuem uma sonda sonora especial para determinar a profundidade do lugar onde se encontram. Essa sonda envia uma onda sonora que bate no fundo do mar e o retorno é ouvido após alguns segundos.
Um navio enviou uma onda sonora que levou 0,6 segundos a ser ouvida.
Sabendo que a velocidade de propagação do som na água é de aproximadamente $1,5\times {{10}^{3}}$ metros por segundo, qual é a profundidade da água sob esse navio?
Expresso
|
|
|
|
PÚBLICO Sítio com Matemática
