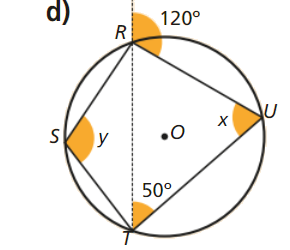
Determina x e y, em cada caso
Circunferência: Matematicamente Falando 9 - Parte 1 Pág. 143 Ex. 9
Enunciado
Determina x e y, em cada caso.
Resolução
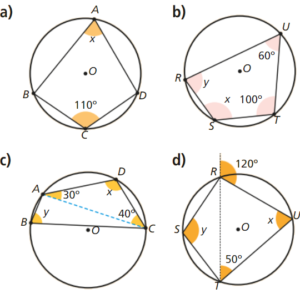
Tendo em consideração que a soma dos ângulos opostos de um quadrilátero inscrito numa circunferência é um ângulo raso, vem:
\[x = B\widehat AD = 180^\circ – B\widehat CD = 180^\circ – 110^\circ = 70^\circ \]Alternativa:
Tendo em consideração que a amplitude de um ângulo inscrito é igual a metade da amplitude do arco compreendido entre os lados do ângulo, vem:
\[x = B\widehat AD = \frac{{\overparen{BCD}}}{2} = \frac{{360^\circ – \overparen{BAD}}}{2} = \frac{{360^\circ – 2 \times B\widehat CD}}{2} = \frac{{360^\circ – 2 \times 110^\circ }}{2} = 70^\circ \]
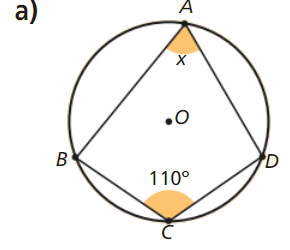
- Tendo em consideração que a soma dos ângulos opostos de um quadrilátero inscrito numa circunferência é um ângulo raso, vem:
\[x = R\widehat ST = 180^\circ – R\widehat UT = 180^\circ – 60^\circ = 120^\circ \]
Finalmente, considerando que a soma das amplitudes dos ângulos internos de um quadrilátero é igual a 360 graus, vem:
\[y = S\widehat RU = 360^\circ – \left( {R\widehat ST + S\widehat TU + T\widehat UR} \right) = 360^\circ – \left( {120^\circ + 100^\circ + 60^\circ } \right) = 80^\circ \]
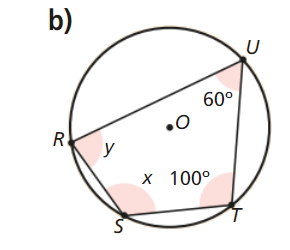
- Como a soma das amplitudes dos ângulos internos de um triângulo é igual a 180 graus, vem:
\[x = A\widehat DC = 180^\circ – \left( {C\widehat AD + A\widehat CD} \right) = 180^\circ – \left( {30^\circ + 40^\circ } \right) = 110^\circ \]
Finalmente, tendo em consideração que a soma dos ângulos opostos de um quadrilátero inscrito numa circunferência é um ângulo raso, vem:
\[y = A\widehat BC = 180^\circ – A\widehat DC = 180^\circ – 110^\circ = 70^\circ \]
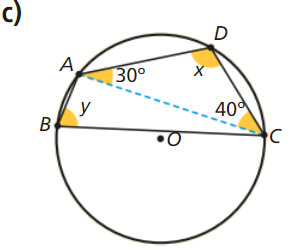
- Tendo em consideração que o ângulo de amplitude 120 graus é um ângulo externo do triângulo [TUR], vem:
\[x = R\widehat UT = 120^\circ – R\widehat TU = 120^\circ – 50^\circ = 70^\circ \]
Finalmente, tendo em consideração que a soma dos ângulos opostos de um quadrilátero inscrito numa circunferência é um ângulo raso, vem:
\[y = R\widehat ST = 180^\circ – R\widehat UT = 180^\circ – 70^\circ = 110^\circ \]
