A Casinha da Matemática Blog
Números inteiros: Matematicamente Falando 7 - Pág. 18 Ex. 5
Enunciado
Usando dois processos, determina:
- $\left( { + 3} \right) \times \left( { – 7} \right) \times \left( { + 2} \right)$
- $\left( { – 4} \right) \times \left( { – 2} \right) \times \left( { – 2} \right)$
- $\left( { + 3} \right) \times \left( { – 2} \right) \times \left( { – 5} \right) \times \left( { + 1} \right)$
- $\left( { + 2} \right) \times \left( { + 5} \right) \times \left( { – 2}
…
Ler mais
Números inteiros: Matematicamente Falando 7 - Pág. 18 Ex. 4
Enunciado
Indica se as igualdades abaixo são verdadeiras ou falsas. Nas verdadeiras indica a propriedade da multiplicação usada. Corrige as falsas.
- $\left( { + 5} \right) \times \left( { – 3} \right) \times \left( { + 2} \right) = \left( { – 3} \right) \times \left( { + 5} \right) \times \left( { + 2} \right)$
- $\left( { – 7} \right) \times \left( { – 2} \right) \times \left( { – 3} \right) = \left( { – 7}
…
Ler mais
Números inteiros: Matematicamente Falando 7 - Pág. 18 Ex. 3
Enunciado
Indica a propriedade da multiplicação utilizada em cada uma das igualdades:
- $ – 5 \times 3 = 3 \times \left( { – 5} \right)$
- $2 \times \left[ {5 \times \left( { – 2} \right)} \right] = \left( {2 \times 5} \right) \times \left( { – 2} \right)$
- $7 \times \left( { – 5} \right) + 7 \times 6 = 7 \times \left( { – 5 + 6} \right)$
- $0 \times \left( { – 3} \right) = 0$
…
Ler mais
Números inteiros: Matematicamente Falando 7 - Pág. 18 Ex. 2
Enunciado
Calcula, por dois processos diferentes:
- $2 \times \left( { – 5 – 1} \right)$
- $ – 3 \times \left( { – 2 + 7} \right)$
- $4 \times \left( {10 – 2} \right)$
- $ – 5 \times \left( { – 3 + 6} \right)$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 31
Enunciado
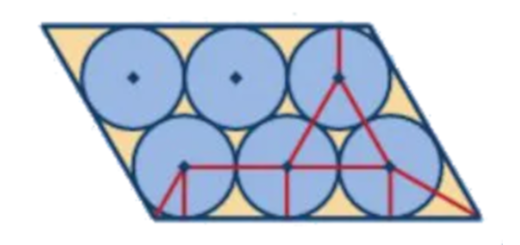
Imagine que alguém pensou acondicionar latas de $75$ cl de refrigerante numa caixa prismática cuja base é um paralelogramo obliquângulo, como mostra a figura.
- Se o raio da base de cada lata medir $4$ cm, qual é a área da base da caixa?
Sugestão: No esquema, marcaram-se vários raios de circunferências. Recorrendo aos seus conhecimentos sobre triângulos (acutângulos ou retângulos) ou ao Teorema de Pitágoras, determine o comprimento e a altura do paralelogramo.
- As latas têm
…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 30
Enunciado
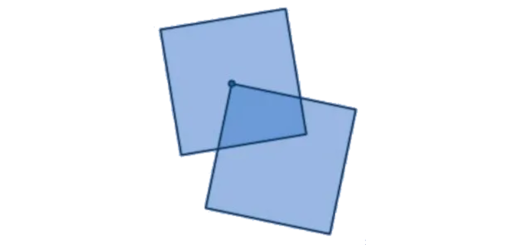
Dois quadrados congruentes de $6$ cm de lado estão sobrepostos como mostra a figura.
O vértice de um dos quadrados está no centro do outro quadrado.
Qual é a área da parte sobreposta?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 30
Enunciado
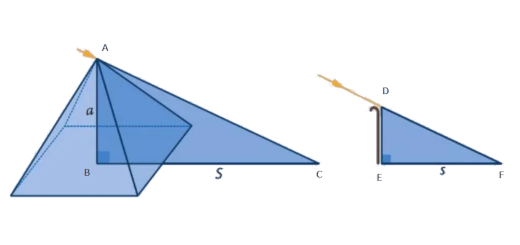
Conta-se que Thales de Mileto (séc. VI a.C.), considerado por alguns autores como um dos sete sábios da Antiguidade, se ofereceu para determinar a altura da pirâmide de Quéops, sem escalar o monumento.
Segundo a lenda, a prova ter-se-á realizado na presença do faraó Amasis. Thales espetou perpendicularmente ao chão a sua bengala e mediu as sombras da bengala e da pirâmide. Após os cálculos rápidos, Thales obteve a resposta desejada.
Em que se baseou o … Ler mais
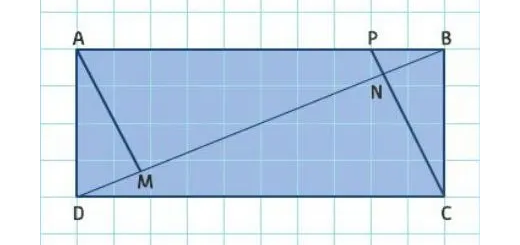
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 29
Enunciado
Observe a figura ao lado, onde [ABCD] é um retângulo.
- Se o segmento de reta [AM] é perpendicular a BD, demonstre que os triângulos [MAD] e [ABD] são semelhantes.
- Se AM e PC são paralelas e AM e BD são perpendiculares, demostre que os triângulos [MAD] e [PBC] são semelhantes e conclua que $\frac{{\overline {AD} }}{{\overline {PC} }} = \frac{{\overline {MD} }}{{\overline {BP} }}$.
- Se PC é perpendicular a BD, demonstre que $\frac{{\overline {NC} }}{{\overline {NB} }}
…
Ler mais
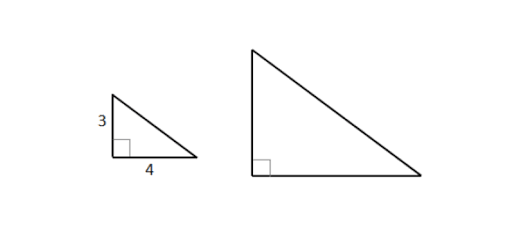
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 28
Enunciado
Determine a medida da hipotenusa de um triângulo retângulo de perímetro igual a $24$ cm que é semelhante a outro cujos catetos medem $3$ cm e $4$ cm.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 27
Enunciado
Os raios de duas circunferências concêntricas medem $4$ cm e $5$ cm.
Determine o comprimento da corda da circunferência maior que é tangente à circunferência menor.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 26
Enunciado
Resolva, em $\mathbb{R}$, as seguintes equações:
- $$\frac{{2\left( {x + 1} \right)}}{3} + 5\left( {x + 2} \right) = 8 – 3x$$
- $$3\left( {\frac{{x + 1}}{2} + \frac{{x – 1}}{3}} \right) = 5x – 2$$
- $$5 – \frac{{2\left( {x + 1} \right)}}{4} = \frac{{3x – 1}}{7}$$
- $$\frac{{x + 4}}{6} – \frac{{2\left( {x + 1} \right)}}{9} = \frac{{x – 2}}{6} + \frac{{11 – 2x}}{{18}}$$
- $$\left( {3x – \frac{2}{3}} \right)\left( {3x + \frac{2}{3}} \right) – 4 = {\left( {3x –
…
Ler mais
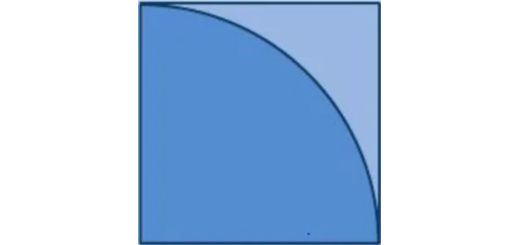
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 25
Enunciado
Quanto mede, com aproximação às décimas, o lado do quadrado, sabendo que a área da parte mais clara é, aproximadamente, $4,35$ m2?
Resolução >>
Resolução
<< Enunciado…
Ler mais
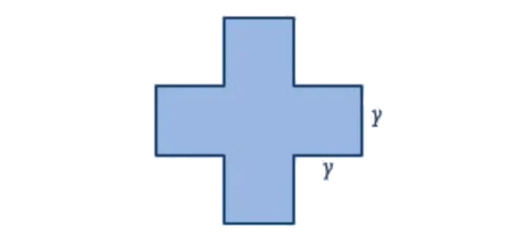
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 37 Ex. 24
Enunciado
Qual deve ser o valor de $y$ para que a área da figura seja $845$ m2?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 37 Ex. 23
Enunciado
Aumentou-se igualmente os lados do retângulo da figura ao lado.
De quanto deve ser o aumento para que a área duplique?
Resolução >>
Resolução
<< Enunciado…
Ler mais















![A área do triângulo [ABC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/04/9V2Pag62-15a-720x340.png)






