A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)
A parte da figura sombreada a verde tem 22 cm2 de área.
Qual é o comprimento, em centímetros, do lado do quadrado [ABCD]? Explica a tua resposta.
Resolução >> Resolução
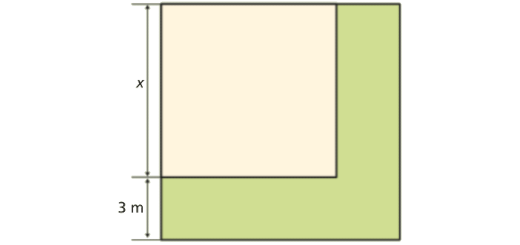
<< Enunciado… Ler maisÀ volta do canteiro quadrado das rosas, o Manuel quer construir uma calçada com 3 m de largura.
Quando foi comprar as lajes para a calçada viu que esta tinha 33 m2 de área.
Qual é a área do terreno destinado às rosas? Explica a tua resposta.
Resolução >> Resolução
<< Enunciado… Ler maisDetermina o conjunto-solução das seguintes equações.
| a) | \(x\left( {x – 1} \right) = 0\) |
| b) | \(\left( {a – 1} \right)\left( {a + 1} \right) = 0\) |
| c) | \({x^2} – 2x = 0\) |
| d) | \(2{x^2} = 32\) |
| e) | \({c^2} – 0,25 = 0\) |
| f) | \({x^2} = 0,01\) |
| g) | \({y^3} – 4y = 0\) |
| h) | \({x^2} – 256 = 0\) |
Resolução >> Resolução
<< Enunciado… Ler maisConstrói uma equação do segundo grau cujo conjunto-solução seja \(\left\{ { – 2,\;2} \right\}\).
Resolução >> Resolução
<< Enunciado… Ler maisResolve as seguintes equações:
| a) | \(4{x^2} = 81\) |
| b) | \(27 – 3{x^2} = 0\) |
| c) | \({\left( {x – 4} \right)^2} + 9 = 0\) |
| d) | \({\left( {x + 3} \right)^2} – 4 = 0\) |
| e) | \({x^2} – 7 = 5{x^2} – 7\) |
| f) | \(16{x^2} – {\left( {x – 1} \right)^2} = 0\) |
Resolução >> Resolução
<< Enunciado… Ler maisDetermina o conjunto-solução de cada uma das equações:
| a) | \({x^2} – 16 = 0\) |
| b) | \(x\left( {{x^2} – 25} \right) = 0\) |
| c) | \(8{x^3} – 2x = 0\) |
| d) | \({x^2} – 36 = 0\) |
| e) | \({\left( {x + 1} \right)^2} – \left( {x + 1} \right) = 0\) |
Resolução >> Resolução
<< Enunciado… Ler maisSe três números naturais m, n e p verificarem a igualdade \({m^2} + {n^2} = {p^2}\) diz-se que \(\left( {m,\;n,\;p} \right)\) é um terno pitagórico.
Associa a cada um dos seguintes polinómios a sua fatorização.
| \(4{x^2} + 12x + 9\) | A | 1 | \({\left( {3x – 2} \right)^2}\) | |
| \({x^2} – 16\) | B | 2 | \({\left( {2x + 3} \right)^2}\) | |
| \(9{x^2} – 12x + 4\) | C | 3 | \(\left( {4x – 1} \right)\left( {4x + 1} \right)\) | |
| \(4{x^2} – 1\) | D | 4 | \(\left( {x + 4} \right)\left( {x – 4} \right)\) | |
| \(4{x^2} – 12x + 9\) | E | 5 | \(\left( {2x – 1} \right)\left( {2x + 1} |
Copia e completa, usando os casos notáveis da multiplicação.
| a) | \(\left( {z – 2} \right)\left( {z + 2} \right) = \ldots – \ldots \) |
| b) | \({\left( {2x + \ldots } \right)^2} = \ldots + 20x + \ldots \) |
| c) | \({\left( {y + 4} \right)^2} = \ldots + \ldots + \ldots \) |
| d) | \({\left( {x + \ldots } \right)^2} = \ldots + \ldots + 49\) |
| e) | \(\left( {n + \ldots } \right)\left( { \ldots – \ldots } \right) |
Apresenta cada um dos polinómios seguintes na forma reduzida.
| a) | \(15x – {\left( {x + 7} \right)^2}\) |
| b) | \(x\left( {x – 1} \right) – {\left( {x – 2} \right)^2}\) |
| c) | \(\left( {x + 2} \right)\left( {x – 3} \right) + {\left( {x + 1} \right)^2}\) |
| d) | \({\left( {x + \frac{1}{2}} \right)^2} – {\left( {x – \frac{1}{2}} \right)^2} – \frac{3}{4}\left( {x – 1} \right)\left( {x + 1} \right)\) |
| e) | \(2x\left( {{x^2} + 3x – \frac{1}{2}} \right)\) |
| f) | \(\left( |
Calcula:
| a) | \({\left( {x – 1} \right)^2}\) |
| b) | \({\left( {1 – x} \right)^2}\) |
| c) | \({\left( {\frac{{3y}}{2} + 1} \right)^2}\) |
| d) | \({\left( {4x – 3} \right)^2}\) |
| e) | \(\left( {2 – x} \right)\left( {2 + x} \right)\) |
| f) | \(\left( {2xy + \frac{1}{2}} \right)\left( {2xy – \frac{1}{2}} \right)\) |
| g) | \(\left( { – 1 + x} \right)\left( { – 1 – x} \right)\) |
| h) | \(\left( {2x + 1} \right)\left( { – 2x + 1} \right)\) |
Resolução >> Resolução
<< Enunciado… Ler maisDetermina, em cada caso, qual é o polinómio B que deves adicionar a \[A = 6{x^2} – 3x + 1\] para obter:
Resolução >> Resolução
<< Enunciado… Ler maisConsidera os seguintes polinómios.
\(A = 2{x^2} – x – 1\) \(B = – 3{x^2} + 3x\) \(C = 4{x^3} – 3\) \(D = 2x + 6\)
Resolução >> Resolução
<< Enunciado… Ler maisRecordando que chamamos binómio a um polinómio com dois termos e trinómio a um polinómio com três termos, indica o número de termos que obtemos, antes de reduzir os termos semelhantes, quando multiplicamos:
Resolução >> Resolução
<< Enunciado… Ler mais
Expresso
|
|
|
|
PÚBLICO Sítio com Matemática
