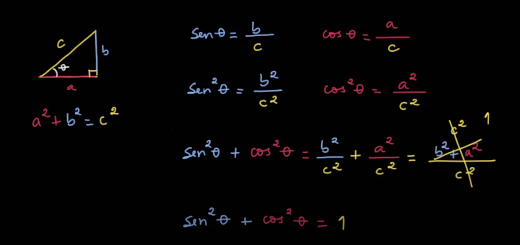Tagged: 11.º Ano

• Enunciado
• Resolução

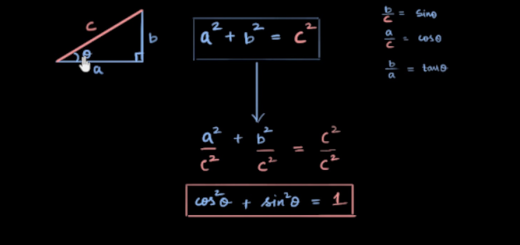
Prove que, para todo o $\theta $, se tem:

1. ${{(sen\,\theta +\cos \theta )}^{2}}=1+2\,sen\,\theta \times \cos \theta $
2. $\cos \theta -se{{n}^{2}}\,\theta \times \cos \theta ={{\cos }^{2}}\theta $
3. $se{{n}^{4}}\,\theta +{{\cos }^{4}}\theta +2\times se{{n}^{2}}\,\theta \times {{\cos }^{2}}\theta =1$
4. ${{(\cos \theta -sen\,\theta )}^{2}}+{{(\cos \theta +sen\,\theta )}^{2}}=2$
5. $(\cos \theta -sen\,\theta )+(\cos \theta +sen\,\theta )-1=-2\times se{{n}^{2}}\,\theta $

Resolução >> Resolução

• Enunciado
• Resolução

1. Sabendo que $tg\,\alpha =\frac{3}{4}$ e $\pi <\alpha <\frac{3\pi }{2}$, determine $sen\,\alpha $ e $\cos \alpha $.
2. Determine $sen\,\alpha $ e $\cos \alpha $, sabendo que $tg\,\alpha =-2$ e $-\frac{\pi }{2}<\alpha <0$.

Resolução >> Resolução

• Enunciado
• Resolução

Sabe-se que $\cos \alpha =\frac{1}{3}$.

1. Determine o valor exato de $sen\,\alpha $ e de $tg\,\alpha $, sabendo que $-\frac{\pi }{2}<\alpha <0$.
2. Determine o valor exato de $sen\,\alpha $ e de $tg\,\alpha $, sabendo que $\frac{3\pi }{2}<\alpha <2\pi $.

Resolução >> Resolução

• Enunciado
• Resolução

Na figura está representado um círculo trigonométrico de centro O e um pentágono regular [ABCDO].

1. Mostre que as coordenadas de B são $(1-\cos \alpha ;sen\,72{}^\text{o})$.
2. Determine uma expressão para obter a área do pentágono em função de $\alpha $ (em graus) e apresente um valor dessa área aproximada às décimas.

Resolução >> Resolução

• Enunciado
• Resolução

Uma professora de Matemática propôs aos seus alunos do 11.º X que encontrassem o melhor valor para a expressão \[sen\,(\frac{5}{6}\pi )-\cos \,(\frac{5}{4}\pi )+2sen\,(-\frac{25}{6}\pi )\]

O Rui, a Sara e a Inês apresentaram os seguintes resultados:

• Rui: $0,21$
• Sara: $\frac{3+\sqrt{2}}{2}$
• Inês: $\frac{\sqrt{2}-1}{2}$

Faça a sua própria pesquisa e comente cada um dos resultados apresentados por aqueles três alunos.

Resolução >> Resolução

• Enunciado
• Resolução

1. Desenhe um ângulo do 2.º quadrante cujo cosseno seja $-\frac{3}{4}$.
   Determine o valor exato do seno e da tangente.
2. Desenhe um ângulo do 4.º quadrante cuja tangente seja $-\frac{3}{2}$.
   Qual o valor exato do seno e do cosseno?

Resolução >> Resolução

• Enunciado
• Resolução

O João e a Maria pretendem determinar a distância da porta A da sua escola à estátua E.

Para isso, espetaram no jardim da escola uma estaca B, a 34 metros de A, e determinaram as amplitudes dos ângulos EAB e ABE, sendo:

• $E\widehat{A}B=26{}^\text{o}$
• $E\widehat{B}A=123{}^\text{o}$

Qual é o valor da distância pretendida?

Resolução >> Resolução

• Enunciado
• Resolução

Num disco de papel de raio 10 cm, desenhe um sector circular.

Faça um corte segundo o segmento [OA]. Ponha cola na parte colorida e sobreponha de forma a fazer coincidir [OA] com [OB]. Obtém assim um cone sem base.

Designe por α a medida, em radianos, do ângulo do sector circular tracejado $(\alpha \in \left] 0,\ 2\pi  \right[)$, por R o raio da circunferência da base do cone e por h a sua altura.

1. 1. Mostre que

• Enunciado
• Resolução

A figura representa uma vista do corte da parede interior de um recipiente cónico, segundo um plano que contém a altura. O ângulo α está expresso em graus e x em centímetros.

1. Seja V(x) o volume do líquido correspondente à parte colorida, expresso em cm³.
   1. Mostre que V(x) é o volume de um cone de raio da base igual a $x.sen\,\frac{\alpha }{2}$ e de altura igual a $x.\cos \,\frac{\alpha }{2}$.
   2. Deduza uma expressão de V(x)

• Enunciado
• Resolução

Uma chaminé de cozinha tem a forma de um tronco de pirâmide com bases retangulares.

As faces [ADHE] e [ABFE] são perpendiculares às duas bases.

Na figura, as dimensões estão expressas em milímetros.

Calcule:

1. as alturas de [BF] e de [DH] dos trapézios [BCGF] e [CDHG], com aproximação ao milímetro;
2. a área de cada uma das faces [BCGF] e [CDHG], com aproximação ao cm²;
3. as medidas dos ângulos α e β, com aproximação à décima