Num disco de papel
Trigonometria: Infinito 11 A - Parte 1 Pág. 90 Ex. 27
Enunciado
Num disco de papel de raio 10 cm, desenhe um sector circular.
Faça um corte segundo o segmento [OA]. Ponha cola na parte colorida e sobreponha de forma a fazer coincidir [OA] com [OB]. Obtém assim um cone sem base.
Designe por α a medida, em radianos, do ângulo do sector circular tracejado $(\alpha \in \left] 0,\ 2\pi \right[)$, por R o raio da circunferência da base do cone e por h a sua altura.
-
- Mostre que $R=\frac{5(2\pi -\alpha )}{\pi }$.
- Verifique que $h=\sqrt{100-{{R}^{2}}}$.
- A que intervalo pertence R e h?
- Considere $\alpha =\frac{4\pi }{5}$ e calcule R e h.
-
- Exprima o volume V do cone em função de R e de h.
- Use a sua calculadora de modo que, para cada valor de α que introduza, ela calcule os valores correspondentes de R e, em seguida, de h e de V.
Existirá um valor de α para o qual o volume seja máximo?
Resolução
- Tendo em consideração que o perímetro da base (Pb) do cone sem base é igual ao comprimento do arco maior AB e que este é diretamente proporcional à amplitude do correspondente ângulo ao centro, temos: \[\begin{matrix}
\frac{2\pi \times 10}{2\pi }=\frac{{{P}_{b}}}{2\pi -\alpha } & \Leftrightarrow & {{P}_{b}}=\frac{20\pi (2\pi -\alpha )}{2\pi } \\
{} & \Leftrightarrow & {{P}_{b}}=10(2\pi -\alpha ) \\
\end{matrix}\]
Assim, obtém-se: \[R=\frac{10(2\pi -\alpha )}{2\pi }=\frac{5(2\pi -\alpha )}{\pi }\]
- Aplicando o Teorema de Pitágoras no triângulo retângulo assinalado na figura, temos: \[h=\sqrt{{{\overline{OA}}^{2}}-{{R}^{2}}}=\sqrt{{{10}^{2}}-{{R}^{2}}}=\sqrt{100-{{R}^{2}}}\]
- $R\in \left] 0,\ 10 \right[$ e $h\in \left] 0,\ 10 \right[$. (Porquê?)
- Para $\alpha =\frac{4\pi }{5}$, obtém-se: \[R(\alpha =\frac{4\pi }{5})=\frac{5(2\pi -\frac{4\pi }{5})}{\pi }=\frac{10\pi -4\pi }{\pi }=6\ (cm)\] e \[h(\alpha =\frac{4\pi }{5})=\sqrt{100-{{6}^{2}}}=8\ (cm)\]
- Tendo em consideração que o perímetro da base (Pb) do cone sem base é igual ao comprimento do arco maior AB e que este é diretamente proporcional à amplitude do correspondente ângulo ao centro, temos: \[\begin{matrix}
-
- Como o volume de um cone é dado por ${{V}_{cone}}=\frac{1}{3}\times {{A}_{b}}\times h$, então \[V=\frac{\pi {{R}^{2}}h}{3}\]
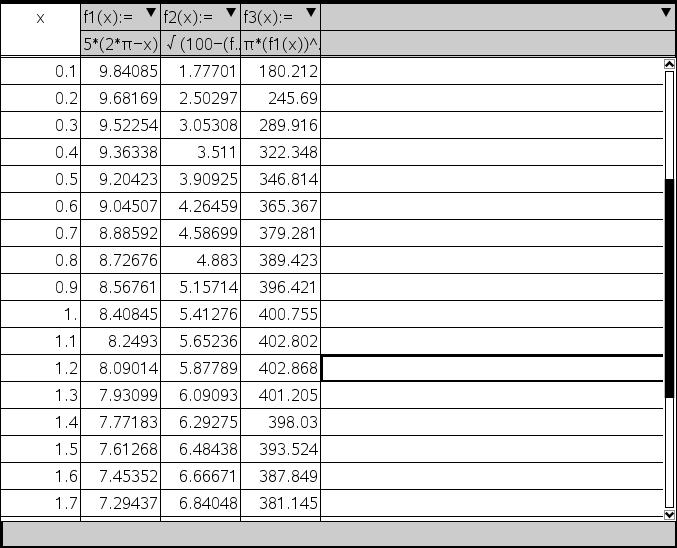
- Definidas as funções \[{{f}_{1}}(x)=\frac{5(2\pi -x)}{\pi }\] \[{{f}_{2}}(x)=\sqrt{100-{{({{f}_{1}}(x))}^{2}}}\] \[{{f}_{3}}(x)=\frac{\pi \times {{({{f}_{1}}(x))}^{2}}\times {{f}_{2}}(x)}{3}\] podemos construir uma tabela de valores, atribuindo a α valores do domínio escolhidos por nós.
Apresenta-se, seguidamente, uma possível tabela de valores.
Por inspeção da tabela, é de admitir a existência de um valor de $\alpha \in \left] 1,1;\ 1,3 \right[$ para o qual o volume é máximo.
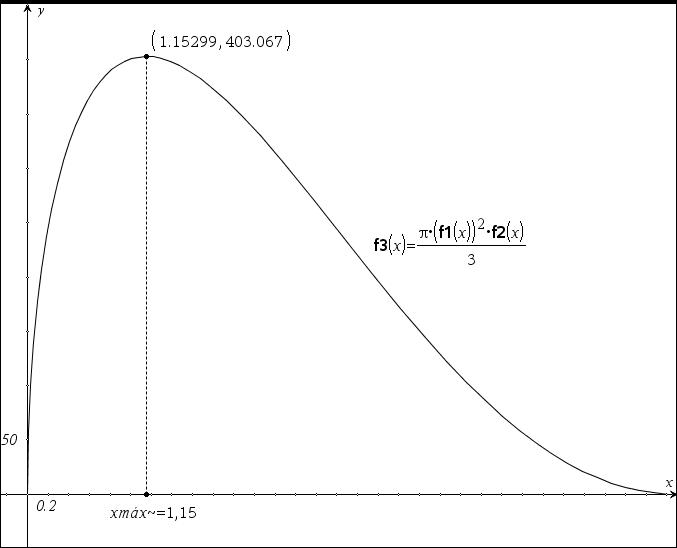
Representando graficamente a função f3 e utilizando as ferramentas adequadas, conclui-se que o maximizante é, aproximadamente, 1,15 radianos:
- Como o volume de um cone é dado por ${{V}_{cone}}=\frac{1}{3}\times {{A}_{b}}\times h$, então \[V=\frac{\pi {{R}^{2}}h}{3}\]
