A representação gráfica de uma função
Funções: Matematicamente Falando 8 - Parte 1 Pág. 72 Ex. 6
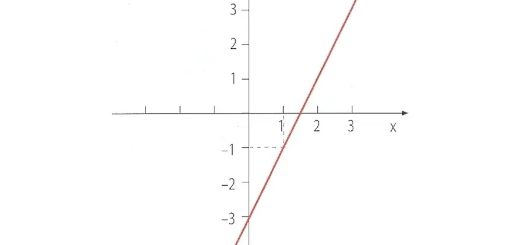
A representação gráfica da função h: $x\to 2x-3$ é:
- Copia e completa:
$h(0)=……$
$h(1)=……$
$h(-1)=……$
$h(2)=……$ - Copia e completa a tabela:
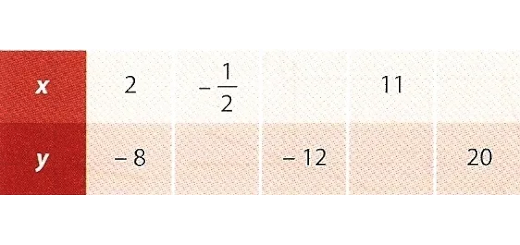
$x$ -1 0 1 2 $2x-3$
Resolução >> Resolução
<< Enunciado… Ler mais