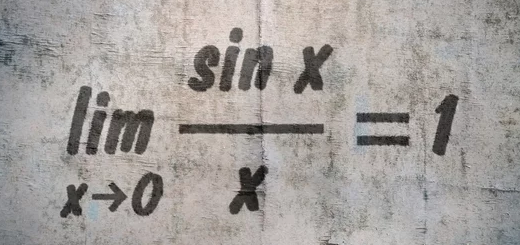A Casinha da Matemática Blog
Equações do 2.º grau: Matematicamente Falando 9 - Pág. 60 Ex. 4
Enunciado
Resolve as seguintes equações:
- $3{x^2} – 7 = 0$
- $2\left( {{x^2} + x} \right) = x$
- $\frac{{13}}{4}{x^2} = \frac{{13}}{5}$
- $2{x^2} + 3 = 0$
- $\frac{4}{7}\left( {x – 2} \right)(x + 2) + x = \frac{{9 + 7x}}{7}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 46 Ex. 18
Enunciado
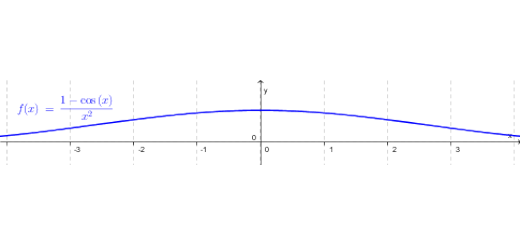
- Determine $${\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{{x^2}}}}$$ multiplicando os termos da fração por $1 + \cos x$.
- Com a sua calculadora gráfica, represente a função $$x \to \frac{{1 – \cos x}}{{{x^2}}}$$ e, recorrendo a um ZOOM perto de zero, verifique o valor obtido na alínea anterior.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 46 Ex. 17
Enunciado
Calcule, se existir:
- $\mathop {\lim }\limits_{x \to 0} \frac{{\operatorname{sen} 3x}}{x}$
- $\mathop {\lim }\limits_{\theta \to 0} \frac{\theta }{{\operatorname{sen} \frac{\theta }{2}}}$
- $\mathop {\lim }\limits_{x \to 0} \frac{{\operatorname{sen} 2x}}{{\operatorname{sen} 3x}}$
- $\mathop {\lim }\limits_{} \left[ {n\operatorname{sen} \left( {\frac{{2\pi }}{n}} \right)} \right]$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 126 Ex. 4
Enunciado
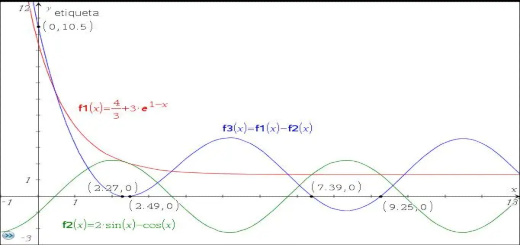
Considere as funções $f$ e $g$ de domínio $\mathbb{R}$, definidas por:
$$f(x) = \frac{4}{3} + 3{e^{(1 – x)}}$$
$$g(x) = 2\operatorname{sen} x – \cos x$$
Utilize métodos exclusivamente analíticos para responder às duas primeiras questões.
- Estude a função $f$ quanto à existência de assíntotas paralelas aos eixos coordenados.
- Resolva a equação $f(x) = g\left( {\frac{{5\pi }}{2}} \right)$ e apresente as soluções na forma $\ln \left( {ke} \right)$, em que $k$ é um número real positivo.
- Recorrendo à
…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 126 Ex. 3
Enunciado
Prendeu-se um carrinho à extremidade C de uma mola horizontal. A outra extremidade da mola está presa num ponto fixo A.
A posição de equilíbrio ocorre quando a mola não está esticada nem comprimida.
Se puxarmos o carrinho e o soltarmos de uma posição um pouco afastada da posição de equilíbrio ele vai oscilar de um lado para o outro em torno da posição de equilíbrio devido à ação da força elástica da mola.
Admitindo que a … Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 125 Ex. 2
Enunciado
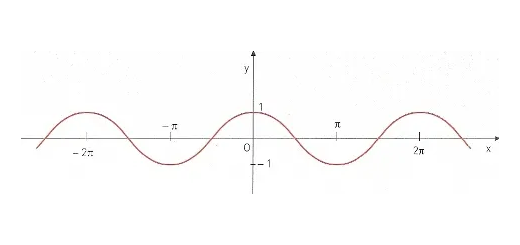
Considere a função real de variável real assim definida: $$f(x) = 1 + 2\cos \left( {x – \frac{\pi }{3}} \right)$$
- O gráfico seguinte representa a função cosseno. Explique como a partir dele obtém o gráfico de $f$.
- Calcule o valor exato de $f\left( {\frac{{7\pi }}{2}} \right) – f\left( {\frac{{7\pi }}{6}} \right)$.
- Determine o contradomínio da função dada.
- Determine uma expressão geral dos zeros da função.
- Averigue se $f(x + 2k\pi ) = f(x),\forall x \in \mathbb{R}$, com
…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 125 Ex. 1
Enunciado
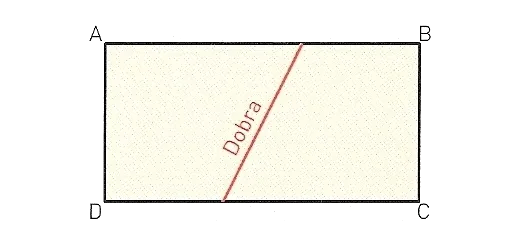
Depois de dobrada uma folha de papel retangular, o vértice A coincide com o vértice C.
Calcule o comprimento do vinco, sabendo que $\overline {AB} = 24\,cm$ e $\overline {AD} = 18\,cm$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 41 Ex. 14
Enunciado
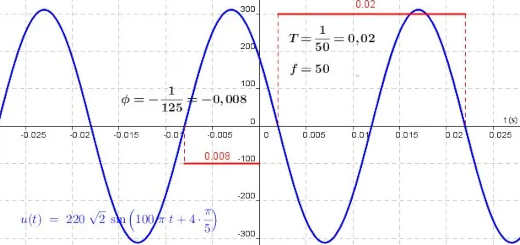
A diferença de potencial, medida em Volt, entre dois pontos de um circuito é dada por:
$$u(t) = 220\sqrt 2 \operatorname{sen} \left( {100\pi t + \frac{4}{5}\pi } \right)$$
($t$ em segundos)
- Mostre que $\frac{1}{{50}}$ é período da função $u$.
- Represente graficamente a função $u$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 36 Ex. 13
Enunciado
Mostre que a função $x \to f(x) = 2\cos \left( {4x + 3\pi } \right)$ é idêntica à função $x \to g(x) = 2\operatorname{sen} \left( {4x – \frac{\pi }{2}} \right)$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 35 Ex. 12
Enunciado
Mostre que $$\operatorname{tg} \left( {2\alpha } \right) = \frac{{2\operatorname{tg} \alpha }}{{1 – {{\operatorname{tg} }^2}\alpha }}$$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 35 Ex. 11
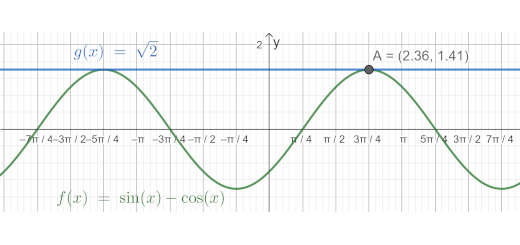
Enunciado
Determine o conjunto solução da equação $\operatorname{sen} \alpha – \cos \alpha = \sqrt 2 $.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 34 Ex. 10
Enunciado
A partir das fórmulas correspondentes do seno e do cosseno, deduza uma fórmula para
- $\operatorname{tg} \left( {\alpha + \beta } \right)$
- $\operatorname{tg} \left( {\alpha – \beta } \right)$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 34 Ex. 9
Enunciado
A partir da fórmula $$\operatorname{sen} \left( {\alpha + \beta } \right) = \operatorname{sen} \alpha \cos \beta + \cos \alpha \operatorname{sen} \beta $$ encontre uma fórmula para:
- $\operatorname{sen} \left( {\alpha – \beta } \right)$
- $\operatorname{sen} \left( {2\alpha } \right)$
Resolução >>
Resolução
<< Enunciado…
Ler mais
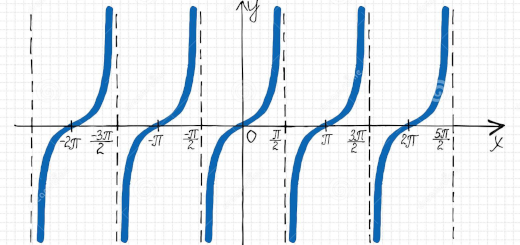
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 33 Ex. 8
Enunciado
Prove que $$\mathop {\lim }\limits_{x \to – \infty } \operatorname{tg} x$$ não existe, encontrando duas sucessões infinitamente grandes, $({u_n})$ e $({v_n})$, tais que $\left( {\operatorname{tg} ({u_n})} \right)$ e $\left( {\operatorname{tg} ({v_n})} \right)$ convirjam para limites diferentes.
Resolução >>
Resolução
<< Enunciado…
Ler mais