A Casinha da Matemática Blog
Função potência: Infinito 11 A - Parte 2 Pág. 209 Ex. 98
Enunciado
A intensidade do som pode ser medida em Watt por metro quadrado, medida da pressão que o som exerce sobre o nosso ouvido. A intensidade do som emitido por uma aparelhagem sonora é função da distância a que o ouvinte se encontra das colunas de som. Na tabela seguinte estão registados os resultados de algumas medições efetuadas a diferentes distâncias das colunas de uma certa aparelhagem de som:
- Descreva o modelo global que relaciona a distância
…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 94
Enunciado
Considere as funções definidas em $\mathbb{R}$ por:
| $f(x)=\frac{3x}{{{x}^{2}}-4}$ |
$f(x)=\frac{{{x}^{2}}}{x+2}$ |
$f(x)=\sqrt{{{x}^{2}}-4}$ |
| $f(x)=\left| {{x}^{2}}-4 \right|$ |
$f(x)=\frac{{{x}^{2}}-4}{{{x}^{2}}}$ |
$f(x)=\frac{{{x}^{3}}}{{{x}^{2}}-9}$
|
- Determine o domínio das funções dadas.
- Calcule, para cada uma delas: $f(-x)$, $f(x-2)$ e $-f(x)$.
- Algumas das funções é par? E ímpar?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 93
Enunciado
A função polinomial definida por $f(x)={{x}^{4}}$ não é injetiva.
Encontre uma restrição g da função f de modo que g seja injetiva.
Caracterize ${{g}^{-1}}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 85
Enunciado
Sendo f e g funções reais de variável real, caracterize $f\circ g$ e $g\circ f$, em cada um dos casos:
- $\begin{matrix}
f(x)=\sqrt{x} & \text{e} & g(x)={{x}^{2}}+1 \\
\end{matrix}$
- $\begin{matrix}
f(x)={{(x-1)}^{3}} & \text{e} & g(x)=\sqrt[3]{x}+1 \\
\end{matrix}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 83
Enunciado
O quadro seguinte dá-nos o sinal de uma função f, definida em $\mathbb{R}$:
Determine o domínio das funções seguintes:
- ${{f}_{1}}:x\to \frac{1}{f(x)}$
- ${{f}_{2}}:x\to \sqrt{f(x)}$
- ${{f}_{3}}:x\to \frac{1}{\sqrt{f(x)}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 82
Enunciado
Determine, em $\mathbb{R}$, o domínio das funções:
- $f:x\to \sqrt{-x}$
- $g:x\to \sqrt{\frac{x-3}{x-4}}$
- $h:x\to \sqrt{-{{x}^{2}}+4x}$
- $i:x\to \frac{\sqrt{x-3}}{\sqrt{x-4}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 81
Enunciado
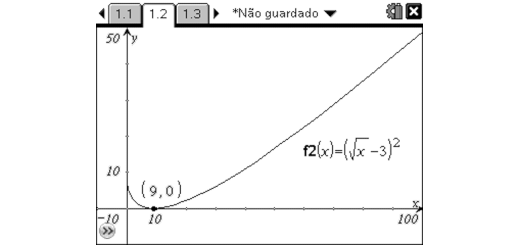
Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to {{(\sqrt{x}+3)}^{2}} & \text{e} & g:x\to {{(\sqrt{x}-3)}^{2}} \\
\end{matrix}\]
- Determine o domínio de f e de g.
- Determine, se existirem, os zeros de f e de g.
- Caracterize as funções $(f+g)$ e $(f\times g)$ e apresente as expressões de $(f+g)(x)$ e $(f\times g)(x)$ na forma mais simplificada possível.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 205 Ex. 80
Enunciado
Verifique se são iguais as funções reais de variável real, f e g, assim definidas:
- $\begin{matrix}
f:x\to \sqrt{{{(-x)}^{2}}} & {} & g:x\to \left| x \right| \\
\end{matrix}$
- $\begin{matrix}
f:x\to \sqrt{x}.\sqrt{x} & {} & g:x\to x \\
\end{matrix}$
- $\begin{matrix}
f:x\to \sqrt{x+1}.\sqrt{x-1} & {} & g:x\to \sqrt{{{x}^{2}}-1} \\
\end{matrix}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 205 Ex. 79
Enunciado
Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to \sqrt{x-2}+1 & {} & g:x\to \sqrt{2{{x}^{2}}-9}-x \\
\end{matrix}\]
- Determine os domínios de f e de g.
- Determine os zeros de cada uma das funções.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Função inversa: Infinito 11 A - Parte 2 Pág. 204 Ex. 75
Enunciado
- Use a calculadora gráfica e conjeture quais das seguintes funções polinomiais têm função inversa:
| ${{f}_{1}}(x)={{x}^{3}}-9{{x}^{2}}+5x-5$ |
${{f}_{2}}(x)=2x+{{x}^{2}}$ |
${{f}_{3}}(x)={{x}^{3}}-2{{x}^{2}}+5x-5$ |
| ${{f}_{4}}(x)=2x-{{x}^{2}}$ |
${{f}_{5}}(x)=2x+{{x}^{3}}$ |
${{f}_{6}}(x)=2x-{{x}^{3}}$ |
- Para as que admitiu serem funções injetivas, calcule a imagem, pela inversa, de 10, com aproximação às centésimas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Função inversa: Infinito 11 A - Parte 2 Pág. 204 Ex. 74
Enunciado
Qual o valor lógico das proposições?
- A função $f:x\to {{x}^{2}}-2$ admite função inversa.
- Nenhuma função par admite função inversa.
- Algumas funções ímpares admitem função inversa.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Função inversa: Infinito 11 A - Parte 2 Pág. 203 Ex. 72
Enunciado
Caracterize a função inversa das seguintes funções de variável real:
- $x\to f(x)=3x+2$
- $x\to g(x)=\frac{2-x}{x}$
- $x\to h(x)=\frac{x-5}{x+2}$
- $x\to i(x)={{x}^{3}}-3$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Função composta: Infinito 11 A - Parte 2 Pág. 203 Ex. 71
Enunciado
Dadas as funções definidas em $\mathbb{R}$ por \[\begin{matrix}
f(x)=3x-4 & e & g(x)=\frac{1}{x} \\
\end{matrix}\]
- Determine:
| $(f+g)(5)$ |
$(f-g)(5)$ |
$(f\times g)(5)$ |
$(f\div g)(5)$ |
| $(f\circ g)(5)$ |
$(g\circ f)(5)$ |
$(f\circ f)(5)$ |
$(g\circ g)(5)$ |
- Caracterize as funções:
| $f+g$ |
$f-g$ |
$f\times g$ |
$f\div g$ |
| $f\circ g$ |
$g\circ f$ |
$f\circ f$ |
$g\circ g$ |
Resolução >>
Resolução
<< Enunciado…
Ler mais
Função composta: Infinito 11 A - Parte 2 Pág. 202 Ex. 66
Enunciado
Sendo $f$ e $g$ funções reais de variável real, caracterize $f\circ g$ e $g\circ f$ em cada um dos casos:
- $\begin{matrix}
f(x)={{x}^{2}}+2x+1 & e & g(x)=3{{x}^{2}}+1 \\
\end{matrix}$
- $\begin{matrix}
f(x)={{x}^{2}}+2x & e & g(x)=\left| x \right|+1 \\
\end{matrix}$
- $\begin{matrix}
f(x)={{x}^{3}} & e & g(x)=\frac{1}{x-3} \\
\end{matrix}$
Resolução >>
Resolução
<< Enunciado…
Ler mais