Category: Aplicando
Decompõe os números
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 6
Enunciado
Decompõe os números $ – 20$ e $12$ num produto de três fatores em que, pelo menos, um deles é um número inteiro negativo.
Resolução >> Resolução
O produto de dois números com o mesmo sinal é um número positivo igual ao produto dos valores absolutos dos fatores. $$\begin{array}{*{20}{c}} {\left( { + 3} \right) \times \left( { + 7} \right) = 21}&{}&{\left( { – 9} \right) \times \left( { – 2} \right) = 18} \end{array}$$
… Ler maisO produto
O que podemos dizer…
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 3
Enunciado
O que podemos dizer…
- do produto de um número por $ + 1$?
- do produto de um número por $ – 1$?
- do produto de um número por $0$?
Resolução >> Resolução
- O produto de um número por $ + 1$ é igual a esse número.
Exemplos: $$\begin{array}{*{20}{c}} {7 \times \left( { + 1} \right) = 7}&{}&{ – 5 \times \left( { + 1} \right) = – 5}&{}&{0 \times \left( { + 1} \right) = 0} \end{array}$$
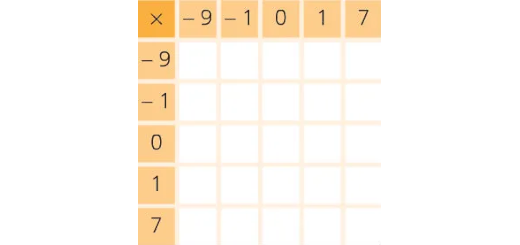
Copia e completa o quadro
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 2
Enunciado
Copia e completa o quadro, calculando os respetivos produtos:
Resolução >> Resolução
<< Enunciado… Ler mais
Escreve as seguintes expressões como multiplicação de números inteiros
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 1
Enunciado
Escreve as seguintes expressões como multiplicação de números inteiros:
- $\left( { – 13} \right) + \left( { – 13} \right) + \left( { – 13} \right)$
- $\left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right)$
- $7 + 7 + 7 + 7$
Resolução >> Resolução
<< Enunciado… Ler mais
Identifique, no conjunto dos pontos do plano, as imagens dos números complexos $z$
Números complexos: Infinito 12 A - Parte 3 Pág. 144 Ex. 64
Enunciado
Identifique, no conjunto dos pontos do plano, as imagens dos números complexos $z$, tais que:
- $\left| {z + 1 + 2i} \right| = 2$
- $\left| {z – i + 2} \right| \leqslant 3$
- $\left| {z + 2 – 4i} \right| = \left| {2i – z} \right|$
- $\left| {\frac{1}{z}} \right| < \frac{1}{4}$
- $z.\overline z = z + \overline z $
- $2\left| {{\text{z – 1}}} \right| \leqslant \left| {{\text{z + 2}}} \right|$
- $\operatorname{Im} \left( {\frac{1}{{z + 1}}} \right) \geqslant
Determine uma equação cartesiana do lugar geométrico
Números complexos: Infinito 12 A - Parte 3 Pág. 108 Ex. 66
Enunciado
Determine uma equação cartesiana do lugar geométrico definido por $\left| {z – i} \right| = \left| {z – \left( { – 1 – i} \right)} \right|$ no plano de Argand.
(Faça $z = x + yi$)
Resolução >> Resolução
<< Enunciado… Ler mais
Resolva, em $\mathbb{C}$, as equações
Números complexos: Infinito 12 A - Parte 3 Pág. 144 Ex. 63
Enunciado
Resolva, em $\mathbb{C}$, as equações:
- ${z^4}.\overline z = 32i$
- ${z^3} + \left( {\sqrt 3 + i} \right)z = 0$
Resolução >> Resolução
<< Enunciado… Ler mais
Determine as raízes da equação
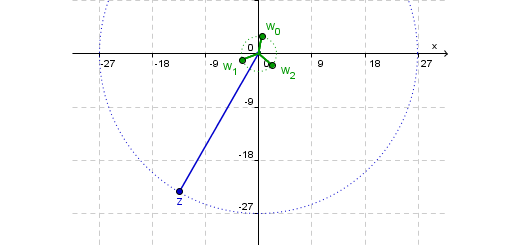
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 62
Enunciado
Dado o número complexo $w = 27\operatorname{cis} \frac{\pi }{3}$, determine as raízes da equação ${z^3} + w = 0$, representando as imagens no plano de Argand.
Resolução >> Resolução
<< Enunciado… Ler mais
Determine, na forma trigonométrica, as raízes da equação ${z^3} – 8i = 0$
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 61
Enunciado
Determine, na forma trigonométrica, as raízes da equação $${z^3} – 8i = 0$$
Resolução >> Resolução
<< Enunciado… Ler mais
As raízes quartas de $1$
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 60
Enunciado
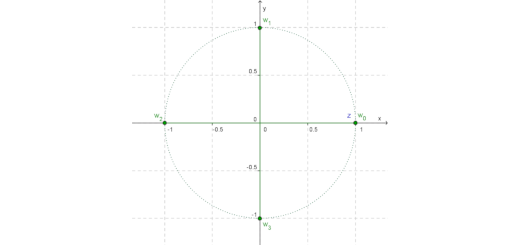
Determine as raízes quartas de $1$ e represente os seus afixos do diagrama de Argand.
Resolução >> Resolução
<< Enunciado… Ler mais
Determine o menor valor inteiro positivo $k$ para o qual ${\left( {\sqrt 3 – i} \right)^k}$ representa um número real positivo
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 59
Enunciado
Determine o menor valor inteiro positivo $k$ para o qual ${\left( {\sqrt 3 – i} \right)^k}$ representa um número real positivo.
Resolução >> Resolução
<< Enunciado… Ler mais
Uma raiz cúbica de um número complexo
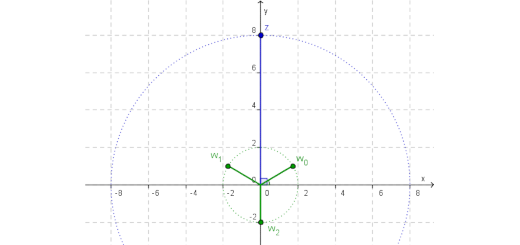
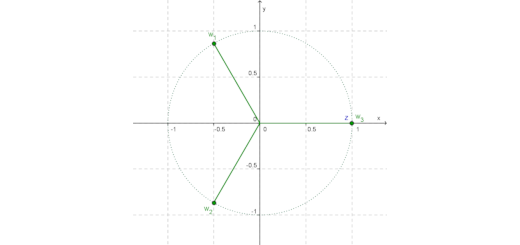
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 58
Enunciado
${w_1} = \frac{{ – 1 + \sqrt 3 i}}{2}$ é uma raiz cúbica de um número complexo $z$.
- Determine as outras raízes cúbicas de $z$.
- Determine $z$.
Resolução >> Resolução
<< Enunciado… Ler mais
Resolva, em $\mathbb{C}$, as equações
Números complexos: Infinito 12 A - Parte 3 Pág. 105 Ex. 65
Enunciado
Resolva, em $\mathbb{C}$, as equações:
- $z – \frac{{2i}}{z} = 0$
- ${z^3} – i{z^2} – z + i = 0$
Resolução >> Resolução
<< Enunciado… Ler mais
