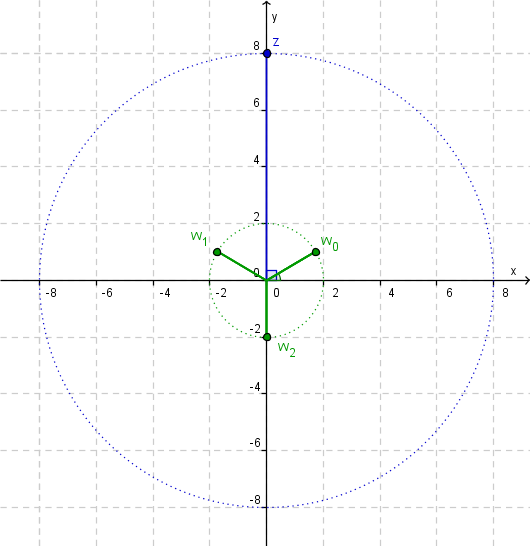
Determine, na forma trigonométrica, as raízes da equação ${z^3} – 8i = 0$
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 61
Determine, na forma trigonométrica, as raízes da equação $${z^3} – 8i = 0$$
$$\begin{array}{*{20}{l}}
{{z^3} – 8i = 0}& \Leftrightarrow &{{z^3} = 8i} \\
{}& \Leftrightarrow &{{z^3} = 8\operatorname{cis} \frac{\pi }{2}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{z = \sqrt[3]{8}\operatorname{cis} \left( {\frac{{\tfrac{\pi }{2}}}{3}} \right)}& \vee &{z = \sqrt[3]{8}\operatorname{cis} \left( {\frac{{\tfrac{\pi }{2}}}{3} + \frac{{2\pi }}{3}} \right)}& \vee &{z = \sqrt[3]{8}\operatorname{cis} \left( {\frac{{\tfrac{\pi }{2}}}{3} + \frac{{4\pi }}{3}} \right)}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{z = 2\operatorname{cis} \left( {\frac{\pi }{6}} \right)}& \vee &{z = 2\operatorname{cis} \left( {\frac{{5\pi }}{6}} \right)}& \vee &{z = 2\operatorname{cis} \left( {\frac{{3\pi }}{2}} \right)}
\end{array}}
\end{array}$$