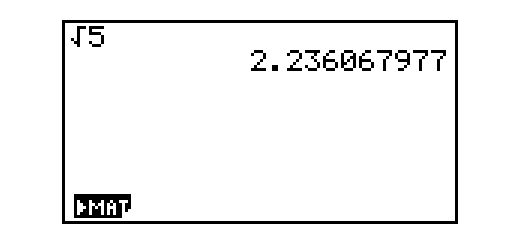Considere as funções

$f(x) = 2\operatorname{sen} x$

• a expressão geral dos zeros

$$\begin{array}{*{20}{l}}
{f(x) = 0}& \Leftrightarrow &{2\operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{x = k\pi ,k \in \mathbb{Z}}
\end{array}$$

• os extremos e a expressão dos minimizantes e maximizantes

Mínimo: $- 2$

$$\begin{array}{*{20}{l}}
{f(x) =  – 2}& \Leftrightarrow &{2\operatorname{sen} x =  – 2} \\
{}& \Leftrightarrow &{\operatorname{sen} x =  – 1} \\
{}& \Leftrightarrow &{x = \frac{{3\pi }}{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

Máximo: $2$

$$\begin{array}{*{20}{l}}
{f(x) = 2}& \Leftrightarrow &{2\operatorname{sen} x = 2} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{x = \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

• o contradomínio

$$D{‘_f} = \left[ { – 2,2} \right]$$

• o período positivo mínimo

Período positivo mínimo: $2\pi $
­

 $g(x) =  – 0,5\operatorname{sen} x$

•  a expressão geral dos zeros

$$\begin{array}{*{20}{l}}
{g(x) = 0}& \Leftrightarrow &{ – 0,5\operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{x = k\pi ,k \in \mathbb{Z}}
\end{array}$$

• os extremos e a expressão dos minimizantes e maximizantes

Mínimo: $ – \frac{1}{2}$

$$\begin{array}{*{20}{l}}
{g(x) =  – \frac{1}{2}}& \Leftrightarrow &{ – 0,5\operatorname{sen} x =  – \frac{1}{2}} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{x = \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

Máximo: $\frac{1}{2}$

$$\begin{array}{*{20}{l}}
{g(x) = \frac{1}{2}}& \Leftrightarrow &{ – 0,5\operatorname{sen} x = \frac{1}{2}} \\
{}& \Leftrightarrow &{\operatorname{sen} x =  – 1} \\
{}& \Leftrightarrow &{x = \frac{{3\pi }}{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

• o contradomínio

$$D{‘_g} = \left[ { – \frac{1}{2},\frac{1}{2}} \right]$$

• o período positivo mínimo

Período positivo mínimo: $2\pi $
­

$h(x) =  – 1 + \operatorname{sen} x$

• a expressão geral dos zeros

$$\begin{array}{*{20}{l}}
{h(x) = 0}& \Leftrightarrow &{ – 1 + \operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{x = \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

• os extremos e a expressão dos minimizantes e maximizantes

Mínimo: $ – 2$

$$\begin{array}{*{20}{l}}
{h(x) =  – 2}& \Leftrightarrow &{ – 1 + \operatorname{sen} x =  – 2} \\
{}& \Leftrightarrow &{\operatorname{sen} x =  – 1} \\
{}& \Leftrightarrow &{x = \frac{{3\pi }}{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

Máximo: $0$

$$\begin{array}{*{20}{l}}
{h(x) = 0}& \Leftrightarrow &{ – 1 + \operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{x = \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

• o contradomínio

$$D{‘_h} = \left[ { – 2,0} \right]$$

• o período positivo mínimo

Período positivo mínimo: $2\pi $
­

$t(x) =  – 1 + 2\operatorname{sen} x$

• a expressão geral dos zeros

$$\begin{array}{*{20}{l}}
{t(x) = 0}& \Leftrightarrow &{ – 1 + 2\operatorname{sen} x = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} x = \frac{1}{2}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x = \frac{\pi }{6} + 2k\pi }& \vee &{x = \frac{{5\pi }}{6} + 2k\pi ,k \in \mathbb{Z}}
\end{array}}
\end{array}$$

• os extremos e a expressão dos minimizantes e maximizantes

Mínimo: $ – 3$

$$\begin{array}{*{20}{l}}
{t(x) =  – 3}& \Leftrightarrow &{ – 1 + 2\operatorname{sen} x =  – 3} \\
{}& \Leftrightarrow &{\operatorname{sen} x =  – 1} \\
{}& \Leftrightarrow &{x = \frac{{3\pi }}{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

Máximo: $1$

$$\begin{array}{*{20}{l}}
{t(x) = 1}& \Leftrightarrow &{ – 1 + 2\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{\operatorname{sen} x = 1} \\
{}& \Leftrightarrow &{x = \frac{\pi }{2} + 2k\pi ,k \in \mathbb{Z}}
\end{array}$$

• o contradomínio

$$D{‘_t} = \left[ { – 3,1} \right]$$

• o período positivo mínimo

Período positivo mínimo: $2\pi $