Um fio encontra-se suspenso entre dois postes
Cálculo diferencial: Infinito 12 A - Parte 2 Pág. 230 Ex. 96
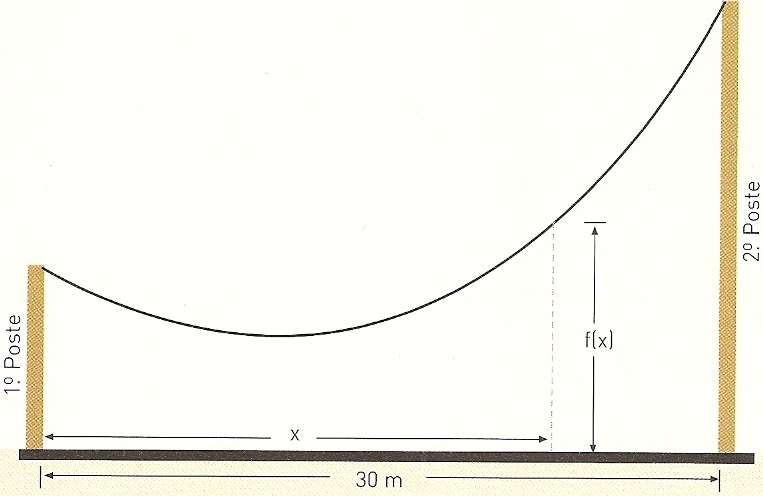
Um fio encontra-se suspenso entre dois postes. A distância entre ambos é de 30 metros.
Considere a função $f$ definida por $$f(x) = 5\left( {{e^{1 – 0,1x}} + {e^{0,1x – 1}}} \right)$$
Admita que $f(x)$ é a distância ao solo, em metros, do ponto do fio a $x$ metros à direita do primeiro poste.
- Determine a diferença de alturas dos dois postes. Apresente o resultado na forma de dízima, com aproximação às décimas.
- Recorrendo ao estudo da derivada da função $f$, determine a distância ao primeiro poste do ponto do fio mais próximo do solo.
- Determine, com aproximação à décima de metro, a distância ao primeiro poste dos pontos do fio que se encontrem a 15 metros do solo.
Considere a função $f$ definida por $$f(x) = 5\left( {{e^{1 – 0,1x}} + {e^{0,1x – 1}}} \right)$$
Admita que $f(x)$ é a distância ao solo, em metros, do ponto do fio a $x$ metros à direita do primeiro poste.
- A diferença de alturas dos dois postes é, aproximadamente, $\Delta h = f(30) – f(0) = 5\left( {{e^{ – 2}} + {e^2}} \right) – 5\left( {{e^1} + {e^{ – 1}}} \right) \approx 22,2$ metros.
- Ora, \[\begin{array}{*{20}{l}}
{f'(x)}& = &{{{\left[ {5\left( {{e^{1 – 0,1x}} + {e^{0,1x – 1}}} \right)} \right]}^\prime }} \\
{}& = &{5\left( { – 0,1 \times {e^{1 – 0,1x}} + 0,1 \times {e^{0,1x – 1}}} \right)} \\
{}& = &{0,5\left( {{e^{0,1x – 1}} – {e^{1 – 0,1x}}} \right)}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f'(x) = 0}& \Leftrightarrow &{0,5\left( {{e^{0,1x – 1}} – {e^{1 – 0,1x}}} \right) = 0} \\
{}& \Leftrightarrow &{{e^{0,1x – 1}} = {e^{1 – 0,1x}}} \\
{}& \Leftrightarrow &{0,1x – 1 = 1 – 0,1x} \\
{}& \Leftrightarrow &{x = 10}
\end{array}$$$x$ $0$ $10$ $30$ $f'(x)$ $-$ $0$ $+$ $f(x)$ Máx. rel. $ \searrow $ Mín abs. $ \nearrow $ Máx. abs. É de 10 metros a distância ao primeiro poste do ponto do fio mais próximo do solo.
- Ora, $$\begin{array}{*{20}{l}}
{f(x) = 15}& \Leftrightarrow &{5\left( {{e^{1 – 0,1x}} + {e^{0,1x – 1}}} \right) = 15} \\
{}& \Leftrightarrow &{{e^{1 – 0,1x}} + {e^{0,1x – 1}} = 3} \\
{}& \Leftrightarrow &{{e^{1 – 0,1x}} + {e^{0,1x – 1}} – 3 = 0}
\end{array}$$
Fazendo $1 – 0,1x = y$, temos:
$$\begin{array}{*{20}{l}}
{{e^y} + {e^{ – y}} – 3 = 0}& \Leftrightarrow &{{e^y} \times {e^y} + {e^y} \times {e^{ – y}} – 3 \times {e^y} = 0} \\
{}& \Leftrightarrow &{{{\left( {{e^y}} \right)}^2} – 3 \times {e^y} + 1 = 0} \\
{}& \Leftrightarrow &{{e^y} = \frac{{3 \mp \sqrt {9 – 4} }}{2}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{{e^y} = \frac{{3 – \sqrt 5 }}{2}}& \vee &{{e^y} = \frac{{3 + \sqrt 5 }}{2}}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{y = \ln \frac{{3 – \sqrt 5 }}{2}}& \vee &{y = \ln \frac{{3 + \sqrt 5 }}{2}}
\end{array}}
\end{array}$$
Dado que $1 – 0,1x = y \Leftrightarrow x = 10 + 10y$, vem: $$\begin{array}{*{20}{l}}
{f(x) = 15}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x = 10 + 10\ln \frac{{3 – \sqrt 5 }}{2}}& \vee &{x = 10 + 10\ln \frac{{3 + \sqrt 5 }}{2}}
\end{array}}
\end{array}$$
A distância ao primeiro poste dos pontos do fio que se encontrem a 15 metros do solo é ${x_1} = 10 + 10\ln \frac{{3 – \sqrt 5 }}{2} \approx 0,4$ e ${x_2} = 10 + 10\ln \frac{{3 + \sqrt 5 }}{2} \approx 19,6$ metros, respetivamente.