Um paralelepípedo e uma pirâmide
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 68 Ex. 6
Enunciado
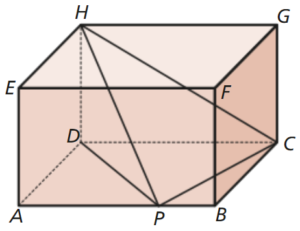Na figura, estão representados um paralelepípedo [ABCDEFGH] e uma pirâmide [HDPC], sendo P um ponto de [AB].
- Qual das afirmações seguintes é verdadeira?
[A] As retas DP e BC são concorrentes.
[B] As retas DP e BC são não complanares.
[C] As retas AB e HG são concorrentes.
[D] As retas AB e HG são não complanares. - Admite que :
– \(\overline {DP} = 5\) cm;
– \(D\widehat PH = 32^\circ \).
Determina a área do triângulo [DPH].
Apresenta o resultado em cm2, arredondado às décimas.
Apresenta os cálculos que efetuares. - Admite que o volume da pirâmide [HDPC] é igual a 10 cm3.
Qual é o volume, em cm3, do paralelepípedo [ABCDEFGH]?
Resolução
A afirmação verdadeira é a [A].
[A] As retas DP e BC são concorrentes.
- No triângulo retângulo [GHP], temos:
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} D\widehat PH = \frac{{\overline {DH} }}{{\overline {DP} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} 32^\circ = \frac{{\overline {DH} }}{5}}\\{}& \Leftrightarrow &{\overline {DH} = 5 \times {\mathop{\rm tg}\nolimits} 32^\circ }\end{array}\]
Portanto, a área do triângulo [DPH], em cm2, arredondado às décimas, é:
\[{A_{\left[ {DPH} \right]}} = \frac{{\overline {DP} \times \overline {DH} }}{2} = \frac{{5 \times 5 \times {\mathop{\rm tg}\nolimits} 32^\circ }}{2} \approx 7,8\] - \({V_{\left[ {ABCDEFGH} \right]}} = 60\) cm3, pois:
\[\frac{{{V_{\left[ {HDPC} \right]}}}}{{{V_{\left[ {ABCDEFGH} \right]}}}} = \frac{{\frac{1}{3} \times {A_{\left[ {CDP} \right]}} \times \overline {DH} }}{{{A_{\left[ {ABCD} \right]}} \times \overline {DH} }} = \frac{{\frac{1}{3} \times \frac{1}{2} \times A\left[ {_{ABCD}} \right] \times \overline {DH} }}{{{A_{\left[ {ABCD} \right]}} \times \overline {DH} }} = \frac{1}{6}\]
![O quadrilátero [ABCD] está dividido em dois triângulos retângulos](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag056-9a-720x340.png)
