Uma função

Seja $f$ a função definida em ${{\mathbb{R}}^{+}}$ por $$f(x)={{\log }_{4}}\left( \frac{{{x}^{2}}}{16} \right)-{{\log }_{4}}x$$

­

1. O domínio da função é: $$\begin{array}{*{35}{l}}
   {{D}_{f}} & = & \left\{ x\in \mathbb{R}:\left( \frac{{{x}^{2}}}{16} \right)>0\wedge x>0 \right\}  \\
   {} & = & \left\{ x\in \mathbb{R}:x\ne 0\wedge x>0 \right\}  \\
   {} & = & {{\mathbb{R}}^{+}}  \\
   \end{array}$$

   Ora, $$\begin{array}{*{35}{l}}
   f(x) & = & {{\log }_{4}}\left( \frac{{{x}^{2}}}{16} \right)-{{\log }_{4}}x  \\
   {} & = & {{\log }_{4}}{{x}^{2}}-\log {}_{4}16-{{\log }_{4}}x  \\
   {} & = & 2{{\log }_{4}}x-2-{{\log }_{4}}x  \\
   {} & = & -2+{{\log }_{4}}x  \\
   \end{array}$$
   Logo, $f(x)=-2+{{\log }_{4}}x\,\,,\forall x\in {{\mathbb{R}}^{+}}$.
   ­

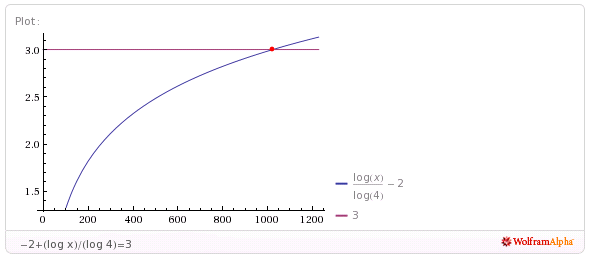
2. Pretende-se determinar a solução da equação: \[\begin{array}{*{35}{l}}
   f(x)=3 & \Leftrightarrow  & \begin{array}{*{35}{l}}
   -2+{{\log }_{4}}x=3 & \wedge  & x\in {{\mathbb{R}}^{+}}  \\
   \end{array}  \\
   {} & \Leftrightarrow  & \begin{array}{*{35}{l}}
   {{\log }_{4}}x=5 & \wedge  & x\in {{\mathbb{R}}^{+}}  \\
   \end{array}  \\
   {} & \Leftrightarrow  & \begin{array}{*{35}{l}}
   x={{4}^{5}} & \wedge  & x\in {{\mathbb{R}}^{+}}  \\
   \end{array}  \\
   {} & \Leftrightarrow  & x=1024  \\
   \end{array}\]
   Portanto, é $1024$ a abcissa do ponto de interseção do gráfico de $f$ com a reta de equação $y=3$.