Uma urna contém seis bolas
Análise combinatória: Infinito 12 A - Parte 1 Pág. 178 Ex. 63
Enunciado
Uma urna contém 6 bolas, cada uma das quais tem uma letra A, B, C, D, E ou F.
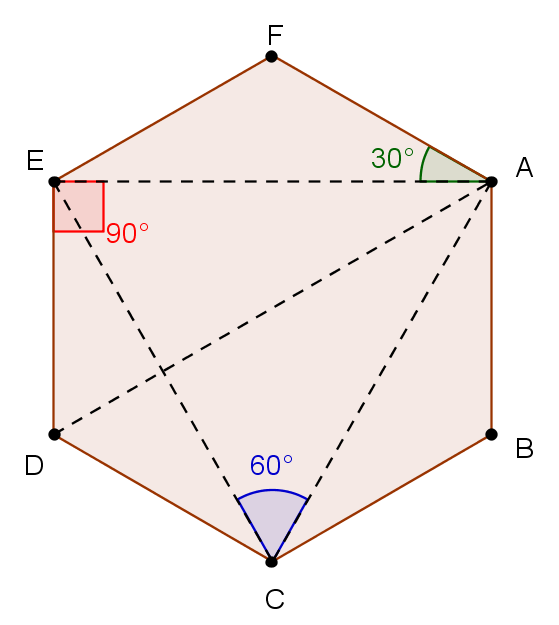
Estas letras são igualmente os vértices do hexágono regular representado ao lado.
- Tiram-se, ao acaso e simultaneamente, três bolas e anotam-se as letras inscritas.
Qual é o espaço de resultados? - A cada extração corresponde um triângulo T, cujos vértices são também vértices do hexágono.
Determine a probabilidade de cada um dos acontecimentos seguintes e descreva, em cada caso, a estratégia de contagem utilizada:
A: “T ser equilátero”;
B: “T ser isósceles, mas não equilátero”;
C: “T ser retângulo”;
D: “T ser um triângulo qualquer”.
Resolução
- Há ${}^{6}{{C}_{3}}=20$ resultados possíveis nesta experiência aleatória, sendo o espaço de resultados: $$\begin{array}{*{35}{l}}
S= & \{(A,B,C), & (A,B,D), & (A,B,E), & (A,B,F), & (A,C,D), \\
{} & (A,C,E), & (A,C,F), & (A,D,E), & (A,D,F), & (A,E,F), \\
{} & (B,C,D), & (B,C,E), & (B,C,F), & (B,D,E), & (B,D,F), \\
{} & (B,E,F), & (C,D,E), & (C,D,F), & (C,E,F), & (D,E,F)\} \\
\end{array}$$ 
$p(A)=\frac{2}{20}=\frac{1}{10}$, pois há apenas dois casos favoráveis: $(A,C,E)$ e $(B,D,F)$.
$p(B)=\frac{6}{20}=\frac{3}{10}$, pois há apenas seis casos favoráveis: os correspondentes a três vértices consecutivos.
$p(C)=\frac{12}{20}=\frac{3}{5}$, pois há apenas doze casos favoráveis: os correspondentes a dois vértices consecutivos e o terceiro vértice diametralmente oposto de um dos dois primeiros.
$p(D)=\frac{20}{20}=1$, pois todos os casos possíveis são favoráveis.
