Três bolas pretas e duas bolas brancas

1. Nesta experiência, o espaço de resultados é $S=\left\{ {{P}_{1}},{{P}_{2}},{{P}_{3}},{{B}_{1}},{{B}_{2}} \right\}$. Logo, $NCP=5$.
   Como há duas maneiras distintas de retirar uma bola branca, então $NCF=2$.
   Logo, a probabilidade de tirar uma bola branca é $P=\frac{2}{5}$.
   ­
2. O acontecimento considerado é impossível, visto haver apenas duas bolas brancas e não se efetuar a reposição da bola extraída. Assim, a probabilidade pedida é nula.
   ­
3. Consideremos o acontecimento X: “tirar três bolas pretas” (em 3 extrações consecutivas, com reposição).
   Comecemos por identificar o conjunto dos casos favoráveis: \[X=\left\{ {{P}_{1}}{{P}_{2}}{{P}_{3}},{{P}_{1}}{{P}_{3}}{{P}_{2}},{{P}_{2}}{{P}_{1}}{{P}_{3}},{{P}_{3}}{{P}_{1}}{{P}_{2}},{{P}_{2}}{{P}_{3}}{{P}_{1}},{{P}_{3}}{{P}_{2}}{{P}_{1}} \right\}\]
   Logo, $NCF=6$.

   Nesta experiência aleatória, o espaço de resultados é bastante numeroso. Então, como contar o número de casos possíveis?
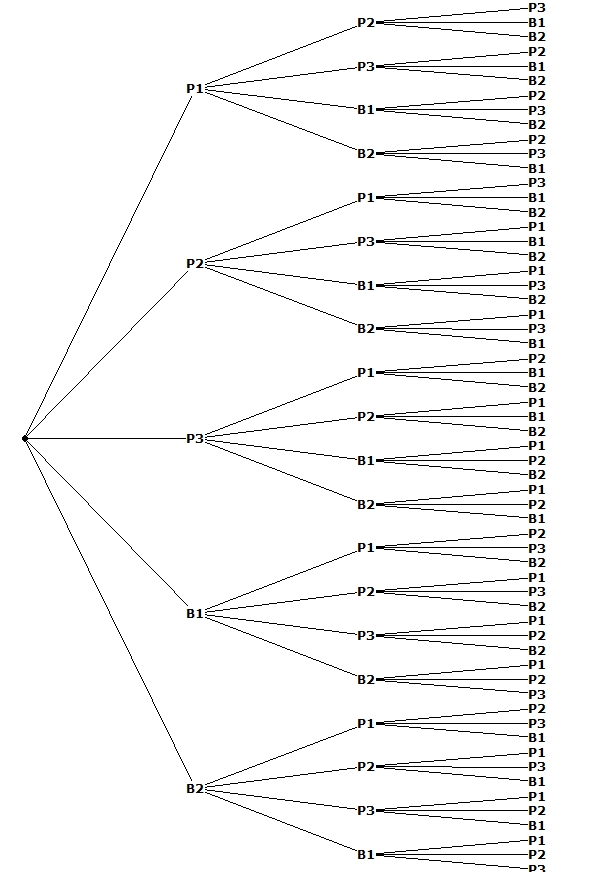
   Uma possibilidade passará por recorrer a um diagrama de árvore, contudo é uma tarefa algo demorada e, por outro lado, esse diagrama ocupará um espaço significativo na folha de papel. (Experimenta!)

   Vamos imaginar apenas como será o aspeto desse diagrama de árvore:

   Relativamente à primeira extração de uma bola do saco, surgem 5 ramos, correspondentes aos cinco resultados possíveis de obter nessa extração (${{P}_{1}},{{P}_{2}},{{P}_{3}},{{B}_{1}},{{B}_{2}}$).

   Quando vamos extrair a segunda bola, há agora apenas quatro bolas dentro do saco, pois a primeira bola extraída não é reposta. Por isso, feita a segunda extração, crescem quatro ramos a partir de cada um dos cinco ramos correspondentes à primeira extração. Assim, após a 2.ª extração a árvore possui $5\times 4=20$ ramos.

   Efetuada a 3.ª extração, crescem 3 ramos (porquê?) a partir de cada um dos 20 ramos correspondentes à segunda extração. Logo, o diagrama em árvore correspondente à experiência em causa possui $20\times 3=60$ ramos.

   Consequentemente, o número de casos possíveis é $NCP=5\times 4\times 3=60$.

   Repara, ainda: \[\begin{matrix}
   NCP & = & \text{5} & \times  & 4 & \times  & 3 & {} & {}  \\
   {} & {} & \Downarrow  & {} & \Downarrow  & {} & \Downarrow  & \Rightarrow  & \text{N}\text{. }\!\!{}^\text{o}\!\!\text{  de possibilidades de extrair a 3}\text{. }\!\!{}^\text{a}\!\!\text{  bola}  \\
   {} & {} & \Downarrow  & {} & \Downarrow  & \Rightarrow  & \Rightarrow  & \Rightarrow  & \text{N}\text{. }\!\!{}^\text{o}\!\!\text{  de possibilidades de extrair a 2}\text{. }\!\!{}^\text{a}\!\!\text{  bola}  \\
   {} & {} & \Downarrow  & \Rightarrow  & \Rightarrow  & \Rightarrow  & \Rightarrow  & \Rightarrow  & \text{N}\text{. }\!\!{}^\text{o}\!\!\text{  de possibilidades de extrair a 1}\text{. }\!\!{}^\text{a}\!\!\text{  bola}  \\
   \end{matrix}\]

   Logo, $P(X)=\frac{6}{60}=\frac{1}{10}$.
   ­

4. A probabilidade pedida é nula, pois o acontecimento considerado é impossível (o saco não contém qualquer bola azul).
   ­
5. A probabilidade pedida é 1, pois o acontecimento considerado é certo. (Porquê?)

Apresenta-se seguidamente o diagrama de árvore considerado na questão 3: