Ângulos internos e externos de um triângulo
Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 102 Ex. 1
Enunciado
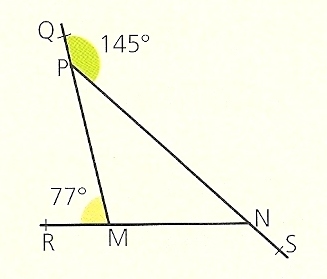Utilizando os dados da figura, calcula:
- A medida de cada um dos ângulos internos do triângulo [MNP];
- A soma dos ângulos externos do triângulo.
Resolução
Considerando que os ângulos seguintes são suplementares, temos:
\[\begin{array}{*{35}{l}}
{\hat{P}} & = & 180{}^\text{o}-N\hat{P}Q \\
{} & = & 180{}^\text{o}-145{}^\text{o} \\
{} & = & 35{}^\text{o} \\
\end{array}\]
e
\[\begin{array}{*{35}{l}}
{\hat{M}} & = & 180{}^\text{o}-N\hat{M}P \\
{} & = & 180{}^\text{o}-77{}^\text{o} \\
{} & = & 103{}^\text{o} \\
\end{array}\]
Como a soma dos ângulos internos de um triângulo é um ângulo raso, vem: \[\begin{array}{*{35}{l}}
{\hat{N}} & = & 180{}^\text{o}-(\hat{M}+\hat{P}) \\
{} & = & 180{}^\text{o}-(103{}^\text{o}+35{}^\text{o}) \\
{} & = & 180{}^\text{o}-138{}^\text{o} \\
{} & = & 42{}^\text{o} \\
\end{array}\]
- Considerando que os ângulos seguintes são suplementares, temos: \[\begin{array}{*{35}{l}}
M\hat{N}S & = & 180{}^\text{o}-\hat{N} \\
{} & = & 180{}^\text{o}-42{}^\text{o} \\
{} & = & 138{}^\text{o} \\
\end{array}\]
Logo, $N\hat{P}Q+R\hat{M}Q+S\hat{N}M=145{}^\text{o}+77{}^\text{o}+138{}^\text{o}=360{}^\text{o}$.
