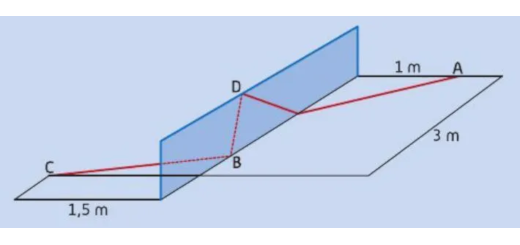
Calcula o valor de x (A)

Consideremos os triângulos [ABH] e [ABC].

Como os triângulos [ABH] e [ABC] são semelhantes (critério AA), os comprimentos dos lados correspondentes são diretamente proporcionais:

\[\frac{{\overline {AB} }}{{\overline {AC} }} = \frac{{\overline {AH} }}{{\overline {AB} }} = \frac{{\overline {BH} }}{{\overline {BC} }}\]

Nota:
Os lados correspondentes, nos dois triângulos, são os lados que se opõem aos ângulos marcados com a mesma cor.

Considerando as duas primeiras razões e substituindo os valores conhecidos, temos:

\[\begin{array}{*{20}{l}}{\frac{6}{{10}} = \frac{{\overline {AH} }}{6}}& \Leftrightarrow &{10 \times \overline {AH} = 6 \times 6}\\{}& \Leftrightarrow &{\overline {AH} = \frac{{6 \times 6}}{{10}}}\\{}& \Leftrightarrow &{\overline {AH} = 3,6}\end{array}\]

Portanto, \(\overline {AH} = 3,6\) cm.