Um muro e uma escada
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 73 Ex. 2
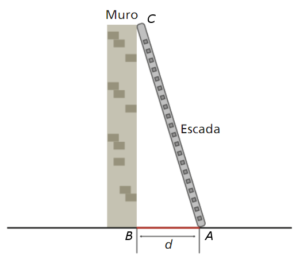 Observa a figura.
Observa a figura.
O muro tem 5 m de altura e a escada tem 5,20 m de comprimento.
- Calcula:
- A distância do pé da escada ao muro.
Escreve essa distância arredondada às décimas. - A medida da amplitude, arredondada às unidades, do ângulo formado pela escada e pelo muro.
- Para que a escada não caia, o ângulo que a escada e o muro fazem deve ter, no máximo, 65 graus. Determina, nesse caso, a altura, arredondada às décimas, a que podemos colocar o topo da escada contra o muro.
Observa a figura.
O muro tem 5 m de altura e a escada tem 5,20 m de comprimento.
- Calcula:
- Aplicando o Teorema de Pitágoras no triângulo retângulo [ABC], temos:
\[d = \overline {AB} = \sqrt {{{\overline {AC} }^2} – {{\overline {BC} }^2}} = \sqrt {{{5,2}^2} – {5^2}} = \sqrt {2,04} \approx 1,4\]
A distância do pé da escada ao muro é, aproximadamente, 1,4 metros.
- No triângulo retângulo [ABC], temos:
\[\begin{array}{*{20}{l}}{\cos A\widehat CB = \frac{{\overline {BC} }}{{\overline {AC} }}}& \Leftrightarrow &{\cos A\widehat CB = \frac{5}{{5,2}}}\\{}& \Leftrightarrow &{A\widehat CB = {{\cos }^{ – 1}}\left( {\frac{5}{{5,2}}} \right)}\\{}&{}&{A\widehat CB \approx 16^\circ }\end{array}\]
É 16 graus a medida da amplitude, arredondada às unidades, do ângulo formado pela escada e pelo muro.
- Na expressão acima, considerando \(A\widehat CB = 65^\circ \), vem:
\[\begin{array}{*{20}{l}}{\cos 65^\circ = \frac{h}{{\overline {AC} }}}& \Leftrightarrow &{\cos 65^\circ = \frac{h}{{5,2}}}\\{}& \Leftrightarrow &{h = 5,2 \times \cos 65^\circ }\\{}&{}&{h \approx 2,2}\end{array}\]
Nesse caso, a altura, arredondada às décimas, a que podemos colocar o topo da escada contra o muro é 2,2 metros, aproximadamente.













![Observa o retângulo [ABCD] da figura](https://www.acasinhadamatematica.pt/wp-content/uploads/2017/10/9V1Pag035-5_520x245.png)




