Relações entre as razões trigonométricas
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 53 Tarefa 5
Enunciado
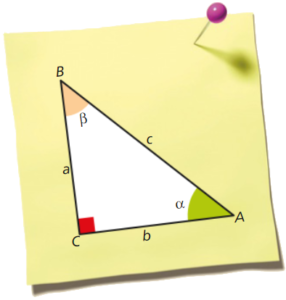
Observa o triângulo [ABC], retângulo em C.
- Como podem relacionar-se os comprimentos a, b e c dos lados do triângulo [ABC]?
 Usando as letras da figura, escreve a razão correspondente a:
Usando as letras da figura, escreve a razão correspondente a:
\({\mathop{\rm sen}\nolimits} \alpha \) \(\cos \alpha \) \({\mathop{\rm tg}\nolimits} \alpha \) \({\mathop{\rm sen}\nolimits} \beta \) \(\cos \beta \) \({\mathop{\rm tg}\nolimits} \beta \) - Usando as razões da alínea anterior, a que é igual:
a) \({\left( {{\mathop{\rm sen}\nolimits} \alpha } \right)^2} + {\left( {\cos \alpha } \right)^2}\)
b) \({\left( {{\mathop{\rm sen}\nolimits} \beta } \right)^2} + {\left( {\cos \beta } \right)^2}\)
O que podemos concluir? - Compara:
a) \(\frac{{{\mathop{\rm sen}\nolimits} \alpha }}{{\cos \alpha }}\) com \({\mathop{\rm tg}\nolimits} \alpha \);
b) \(\frac{{{\mathop{\rm sen}\nolimits} \beta }}{{\cos \beta }}\) com \({\mathop{\rm tg}\nolimits} \beta \). - Que relação existe entre os ângulos de amplitude \(\alpha \) e de amplitude \(\beta \)?
- Compara \({{\mathop{\rm sen}\nolimits} \alpha }\) com \({\cos \beta }\) e \({\cos \alpha }\) com \({{\mathop{\rm sen}\nolimits} \beta }\).
O que podes concluir?
Resolução
Observa o triângulo [ABC], retângulo em C.
- Como podem relacionar-se os comprimentos a, b e c dos lados do triângulo [ABC]?
De acordo com o Teorema de Pitágoras, será: \({a^2} + {b^2} = {c^2}\).  Usando as letras da figura, escreve a razão correspondente a:
Usando as letras da figura, escreve a razão correspondente a:
\[{\mathop{\rm sen}\nolimits} \alpha = \frac{a}{c}\] \[\cos \alpha = \frac{b}{c}\] \[{\mathop{\rm tg}\nolimits} \alpha = \frac{a}{b}\] \[{\mathop{\rm sen}\nolimits} \beta = \frac{b}{c}\] \[\cos \beta = \frac{a}{c}\] \[{\mathop{\rm tg}\nolimits} \beta = \frac{b}{a}\] - Usando as razões da alínea anterior, a que é igual:
a) \({\left( {{\mathop{\rm sen}\nolimits} \alpha } \right)^2} + {\left( {\cos \alpha } \right)^2}\)\( = {\left( {\frac{a}{c}} \right)^2} + {\left( {\frac{b}{c}} \right)^2} = \frac{{{a^2} + {b^2}}}{{{c^2}}} = 1\)
b) \({\left( {{\mathop{\rm sen}\nolimits} \beta } \right)^2} + {\left( {\cos \beta } \right)^2}\)\( = {\left( {\frac{b}{c}} \right)^2} + {\left( {\frac{a}{c}} \right)^2} = \frac{{{a^2} + {b^2}}}{{{c^2}}} = 1\)
O que podemos concluir?
\[\begin{array}{*{20}{c}}{{{\left( {{\mathop{\rm sen}\nolimits} \alpha } \right)}^2} + {{\left( {\cos \alpha } \right)}^2} = 1}&{qualquer\;que\;seja\;\alpha \in \left] {0^\circ ,90^\circ } \right[}\end{array}\] - Compara:
a) \(\frac{{{\mathop{\rm sen}\nolimits} \alpha }}{{\cos \alpha }}\) com \({\mathop{\rm tg}\nolimits} \alpha \);
\(\frac{{{\mathop{\rm sen}\nolimits} \alpha }}{{\cos \alpha }} = \frac{{\frac{a}{c}}}{{\frac{b}{c}}} = \frac{a}{c} \times \frac{c}{b} = \frac{a}{b} = {\mathop{\rm tg}\nolimits} \alpha \)
b) \(\frac{{{\mathop{\rm sen}\nolimits} \beta }}{{\cos \beta }}\) com \({\mathop{\rm tg}\nolimits} \beta \).
\(\frac{{{\mathop{\rm sen}\nolimits} \beta }}{{\cos \beta }} = \frac{{\frac{b}{c}}}{{\frac{a}{c}}} = \frac{b}{c} \times \frac{c}{a} = \frac{b}{a} = {\mathop{\rm tg}\nolimits} \beta \)
\[\begin{array}{*{20}{c}}{{\mathop{\rm tg}\nolimits} \alpha = \frac{{{\mathop{\rm sen}\nolimits} \alpha }}{{\cos \alpha }}}&{qualquer\;que\;seja\;\alpha \in \left] {0^\circ ,90^\circ } \right[}\end{array}\]
- Que relação existe entre os ângulos de amplitude \(\alpha \) e de amplitude \(\beta \)?
Os ângulos de amplitude \(\alpha \) e de amplitude \(\beta \) são complementares, pois \(\alpha + \beta = 90^\circ \). - Compara \({{\mathop{\rm sen}\nolimits} \alpha }\) com \({\cos \beta }\) e \({\cos \alpha }\) com \({{\mathop{\rm sen}\nolimits} \beta }\).
Comparando, verificamos que \({\mathop{\rm sen}\nolimits} \alpha = \frac{a}{c} = \cos \beta \) e que \(\cos \alpha = \frac{b}{c} = {\mathop{\rm sen}\nolimits} \beta \).
O que podes concluir?
\[\begin{array}{*{20}{c}}{{\mathop{\rm sen}\nolimits} \left( {90^\circ – \alpha } \right) = \cos \alpha }&e&{\cos \left( {90^\circ – \alpha } \right) = {\mathop{\rm sen}\nolimits} \alpha }\end{array}\]













![O triângulo [MAR] é retângulo](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/01/9V1Pag129-5_520x245.png)




