Um ponto $B$
Funções racionais: Aleph 11 - Volume 2 Pág. 49 Ex. 9
Seja $B$ o ponto de coordenadas $\left( {1,2} \right)$.
A cada ponto $C\left( {x,0} \right)$ do eixo $Ox$, com $x > 1$, faça corresponder um ponto $D\left( {0,y} \right)$ do eixo $Oy$, de modo que $B$, $C$ e $D$ sejam colineares.
- Exprima $y$ em função de $x$.
- Mostre que a área $A\left( x \right)$ do triângulo $\left[ {ODC} \right]$ é dada por: \[A\left( x \right) = \frac{{{x^2}}}{{x – 1}},\,x > 1\]
- Represente o gráfico de $A$ e indique o maior intervalo onde $A$ é crescente e o maior intervalo onde é decrescente.
- Determine para que valores de $x$ se verifica $A\left( x \right) > 8$.
- Seja $B’$ a projeção ortogonal de $B$ sobre o eixo $Ox$.
Como os triângulos $\left[ {COD} \right]$ e $\left[ {CB’B} \right]$ são semelhantes, para $x > 1$ vem: \[\frac{{\overline {DO} }}{{\overline {BB’} }} = \frac{{\overline {OC} }}{{\overline {B’C} }} \Leftrightarrow \frac{y}{2} = \frac{x}{{x – 1}} \Leftrightarrow \boxed{y = \frac{{2x}}{{x – 1}}}\]
- Para $x > 1$, a área do triângulo $\left[ {ODC} \right]$ é dada por: \[\begin{array}{*{20}{l}}
{A\left( x \right)}& = &{\frac{{\overline {OC} \times \overline {OD} }}{2}} \\
{}& = &{\frac{{x \times \frac{{2x}}{{x – 1}}}}{2}} \\
{}& = &{\frac{{{x^2}}}{{x – 1}}}
\end{array}\]Na animação acima, arraste o ponto $C$.
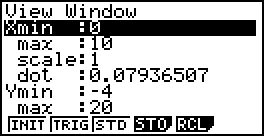
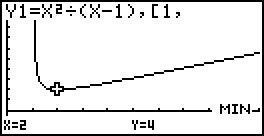
- Apresenta-se, de seguida, uma representação gráfica da função e a indicação da janela de visualização.


De acordo com a indicação fornecida pela ferramenta adequada da calculadora, a função admite $4$ como mínimo absoluto, para $x = 2$.
Assim sendo, a função é decrescente no intervalo $\left] {1,2} \right[$ e crescente no intervalo $\left] {2, + \infty } \right[$.
- Tem-se sucessivamente:
\[\begin{array}{*{20}{l}}
{A\left( x \right) > 8}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{\frac{{{x^2}}}{{x – 1}} > 8}& \wedge &{x > 1}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{{x^2} > 8\left( {x – 1} \right)}& \wedge &{x > 1}&{({\text{pois }}x – 1 > 0)}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{{x^2} – 8x + 8 > 0}& \wedge &{x > 1}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x \in \left] { – \infty ,\frac{{8 – \sqrt {64 – 32} }}{2}} \right[ \cup \left] {\frac{{8 – \sqrt {64 – 32} }}{2}, + \infty } \right[}& \wedge &{x > 1}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x \in \left] { – \infty ,4 – 2\sqrt 2 } \right[ \cup \left] {4 + 2\sqrt 2 , + \infty } \right[}& \wedge &{x > 1}
\end{array}} \\
{}& \Leftrightarrow &{x \in \left] {1,4 – 2\sqrt 2 } \right[ \cup \left] {4 + 2\sqrt 2 , + \infty } \right[}
\end{array}\]