Número de horas de estudo
Funções racionais: Aleph 11 - Volume 2 Pág. 48 Ex. 4
Enunciado
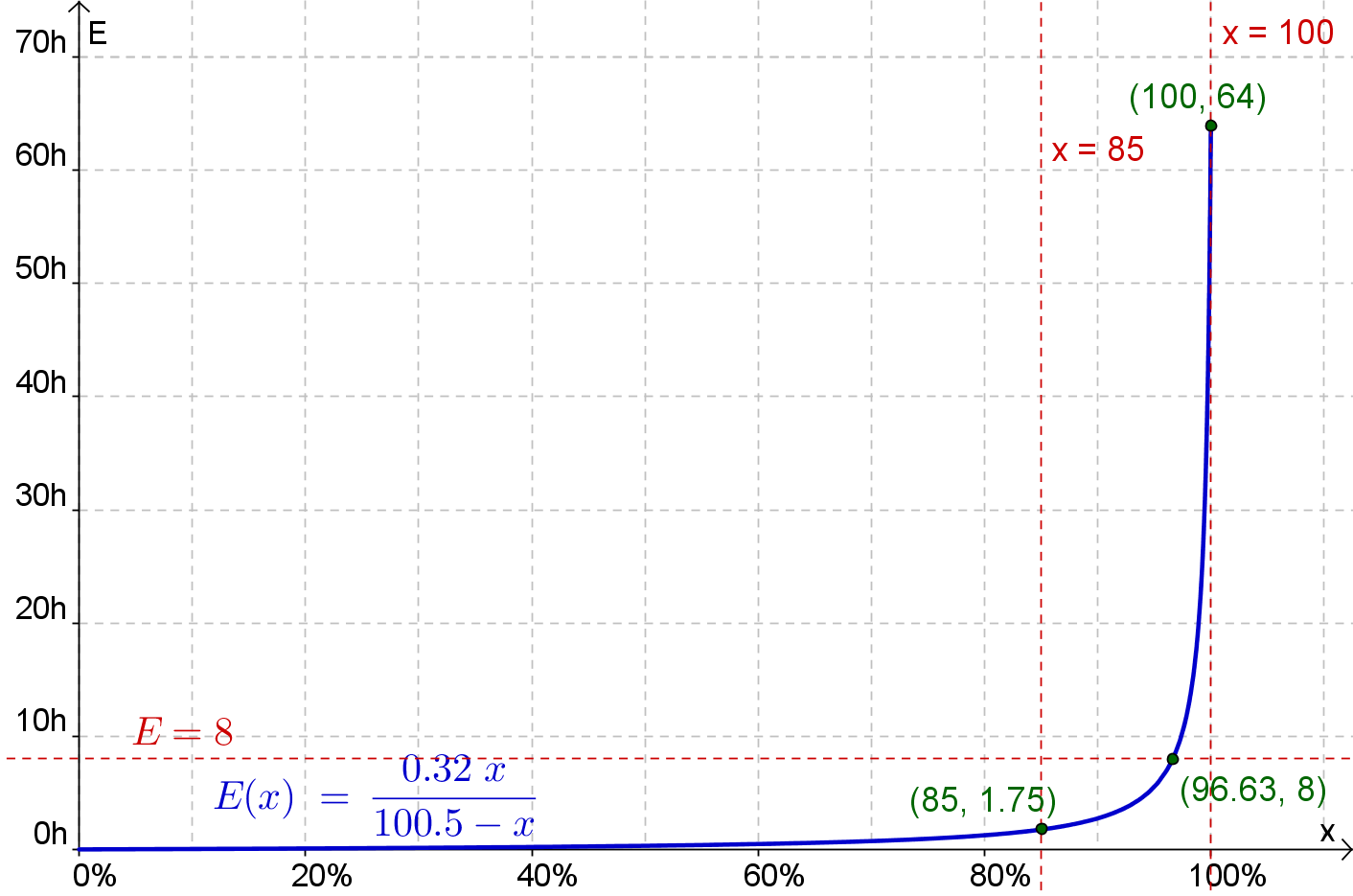
A função \[E\left( x \right) = \frac{{0,32x}}{{100,5 – x}}\] permite determinar o número de horas de estudo, $E\left( x \right)$, necessárias para obter num teste um resultado $x$, entre $0$ e $100$ (em percentagem).
- Quantas horas de estudo são necessárias para se obter $85$ (em percentagem)?
Apresente o resultado em horas e minutos, com aproximação ao minuto. - Qual o resultado (com aproximação às décimas) que se obtém se se estudar $8$ horas?
- Quantas horas de estudo são necessárias para se obter $100$ (em percentagem)?
Resolução
- Como \[E\left( {85} \right) = \frac{{0,32 \times 85}}{{100,5 – 85}} = \frac{{27,2}}{{15,5}} \approx 1,755\] e $0,755 \times 60 = 45,3$, para se obter $85$ (em percentagem) nesse teste, é necessário um estudo de $1$ hora e $45$ minutos, aproximadamente.
- Tem-se sucessivamente:
\[\begin{array}{*{20}{l}}
{E\left( x \right) = 8}& \Leftrightarrow &{\frac{{0,32x}}{{100,5 – x}} = \mathop 8\limits_{\left( {100,5 – x} \right)} } \\
{}& \Leftrightarrow &{\frac{{0,32x + 8x – 804}}{{100,5 – x}} = 0} \\
{}& \Leftrightarrow &{\frac{{8,32x – 804}}{{100,5 – x}} = 0} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{8,32x – 804 = 0}& \wedge &{100,5 – x \ne 0}
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{x = \frac{{804}}{{8,32}}}& \wedge &{x \ne 100,5}
\end{array}} \\
{}& \Leftrightarrow &{x = \frac{{5025}}{{52}}} \\
{}&{}&{x \approx 96,6}
\end{array}\]Se se estudar $8$ horas, obtém-se, aproximadamente, a percentagem de ${96,6}$.
- Como \[E\left( {100} \right) = \frac{{0,32 \times 100}}{{100,5 – 100}} = \frac{{32}}{{0,5}} = 64\] para se obter $85$ (em percentagem) nesse teste, é necessário um estudo de $64$ horas.
Resolução gráfica do problema
