A Casinha da Matemática Blog
Decompõe os números
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 6
Enunciado
Decompõe os números $ – 20$ e $12$ num produto de três fatores em que, pelo menos, um deles é um número inteiro negativo.
Resolução >> Resolução
O produto de dois números com o mesmo sinal é um número positivo igual ao produto dos valores absolutos dos fatores. $$\begin{array}{*{20}{c}} {\left( { + 3} \right) \times \left( { + 7} \right) = 21}&{}&{\left( { – 9} \right) \times \left( { – 2} \right) = 18} \end{array}$$
… Ler maisO produto
O que podemos dizer…
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 3
Enunciado
O que podemos dizer…
- do produto de um número por $ + 1$?
- do produto de um número por $ – 1$?
- do produto de um número por $0$?
Resolução >> Resolução
- O produto de um número por $ + 1$ é igual a esse número.
Exemplos: $$\begin{array}{*{20}{c}} {7 \times \left( { + 1} \right) = 7}&{}&{ – 5 \times \left( { + 1} \right) = – 5}&{}&{0 \times \left( { + 1} \right) = 0} \end{array}$$
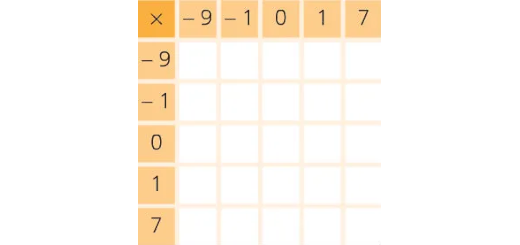
Copia e completa o quadro
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 2
Enunciado
Copia e completa o quadro, calculando os respetivos produtos:
Resolução >> Resolução
<< Enunciado… Ler mais
Escreve as seguintes expressões como multiplicação de números inteiros
Números inteiros: Matematicamente Falando 7 - Pág. 14 Ex. 1
Enunciado
Escreve as seguintes expressões como multiplicação de números inteiros:
- $\left( { – 13} \right) + \left( { – 13} \right) + \left( { – 13} \right)$
- $\left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right) + \left( { – 5} \right)$
- $7 + 7 + 7 + 7$
Resolução >> Resolução
<< Enunciado… Ler mais
Além do Cosmos
National Geographic Chanel - Apresentado por Brian Green
Brian Greene revela um segredo: fomos todos enganados. Nossas percepções de tempo e espaço fizeram com que ficássemos desnorteados.
Muito do que acreditávamos saber sobre nosso universo pode estar errado. Esta série de quatro horas baseada no livro escrito pelo renomado físico e aclamado autor Brian Greene, vai levar-nos aos limites da física para ver como cientistas estão montando a maior imagem até agora do espaço, do tempo e do universo.
A cada passo, vamos descobrir que logo abaixo da … Ler mais
A Busca pela Inteligência Artificial
Horizon - Apresentado por Marcus Du Sautoy
Marcus Du Sautoy wants to find out how close we are to creating machines that can think like us: robots or computers that have artificial intelligence.
His journey takes him to a strange and bizarre world where AI is now taking shape.
Marcus meets two robots who are developing their own private language, and attempts to communicate to them. He discovers how a super computer beat humans at one of the toughest quiz shows on the planet, Jeopardy. And finds … Ler mais
The Story of Electricity
BBC FOUR - Apresentado por Jim Al-Khalili
Professor Jim Al-Khalili tells the story of our quest to master the power of electricity. Ler mais
The Hunt for the Higgs
Horizon - Apresentado por Jim Al-Khalili
Horizon goes behind the scenes at CERN to follow one of the most epic and expensive scientific quests of all time: the search for the Higgs particle, believed to give mass to everything in our universe.
However, the hunt for Higgs is part of a much grander search for how the universe works. It promises to help answer questions like why we exist and is a vital part of a Grand Unified Theory of nature. At the heart of the … Ler mais
Identifique, no conjunto dos pontos do plano, as imagens dos números complexos $z$
Números complexos: Infinito 12 A - Parte 3 Pág. 144 Ex. 64
Enunciado
Identifique, no conjunto dos pontos do plano, as imagens dos números complexos $z$, tais que:
- $\left| {z + 1 + 2i} \right| = 2$
- $\left| {z – i + 2} \right| \leqslant 3$
- $\left| {z + 2 – 4i} \right| = \left| {2i – z} \right|$
- $\left| {\frac{1}{z}} \right| < \frac{1}{4}$
- $z.\overline z = z + \overline z $
- $2\left| {{\text{z – 1}}} \right| \leqslant \left| {{\text{z + 2}}} \right|$
- $\operatorname{Im} \left( {\frac{1}{{z + 1}}} \right) \geqslant
Determine uma equação cartesiana do lugar geométrico
Números complexos: Infinito 12 A - Parte 3 Pág. 108 Ex. 66
Enunciado
Determine uma equação cartesiana do lugar geométrico definido por $\left| {z – i} \right| = \left| {z – \left( { – 1 – i} \right)} \right|$ no plano de Argand.
(Faça $z = x + yi$)
Resolução >> Resolução
<< Enunciado… Ler mais
Resolva, em $\mathbb{C}$, as equações
Números complexos: Infinito 12 A - Parte 3 Pág. 144 Ex. 63
Enunciado
Resolva, em $\mathbb{C}$, as equações:
- ${z^4}.\overline z = 32i$
- ${z^3} + \left( {\sqrt 3 + i} \right)z = 0$
Resolução >> Resolução
<< Enunciado… Ler mais
Determine as raízes da equação
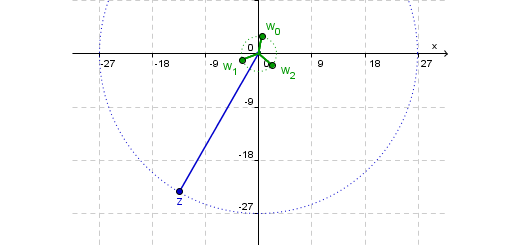
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 62
Enunciado
Dado o número complexo $w = 27\operatorname{cis} \frac{\pi }{3}$, determine as raízes da equação ${z^3} + w = 0$, representando as imagens no plano de Argand.
Resolução >> Resolução
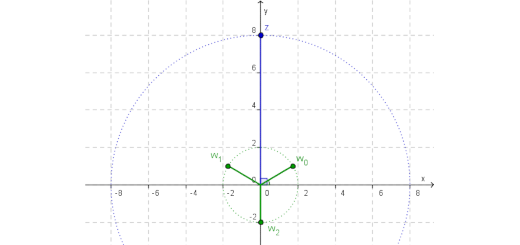
<< Enunciado… Ler mais
Determine, na forma trigonométrica, as raízes da equação ${z^3} – 8i = 0$
Números complexos: Infinito 12 A - Parte 3 Pág. 143 Ex. 61
Enunciado
Determine, na forma trigonométrica, as raízes da equação $${z^3} – 8i = 0$$
Resolução >> Resolução
<< Enunciado… Ler mais
